由代数式的乘法法则类比推导向量的数量积的运算法则：
①“mn＝nm”类比得到“
”；
②“(m＋n)t＝mt＋nt”类比得到“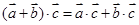
”；
③“(m•n)t＝m(n•t)”类比得到“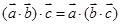
”；
④“t≠0，mt＝xt⇒m＝x”类比得到“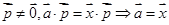
”；
⑤“|m•n|＝|m|•|n|”类比得到“
”；
⑥“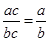
”类比得到“
”．
以上式子中，类比得到的结论正确的个数是( )
| A．1 | B．2 | C．3 | D．4 |
设函数f(x)＝ax2＋bx＋c(a，b，c∈R)，若x＝－1为函数f(x)ex的一个极值点，则下列图象不可能为y＝f(x)的图象是( )．
设函数f(x)＝xex，则( )．
| A．x＝1为f(x)的极大值点 |
| B．x＝1为f(x)的极小值点 |
| C．x＝－1为f(x)的极大值点 |
| D．x＝－1为f(x)的极小值点 |
若S1＝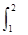
x2dx，S2＝
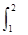dx，S3＝exdx，则S1，S2，S3的大小关系为( )．
| A．S1＜S2＜S3 | B．S2＜S1＜S3 |
| C．S2＜S3＜S1 | D．S3＜S2＜S1 |
函数y＝
x2－ln x的单调减区间是 ( )．
| A．(－1,1] | B．(0,1] | C．[1，＋∞) | D．(0，＋∞) |
设函数f(x)＝
，g(x)＝－x2＋bx，若y＝f(x)的图象与y＝g(x)的图象有且仅有两个不同的公共点A(x1，y1)，B(x2，y2)，则下列判断正确的是 ( )．
| A．x1＋x2＞0，y1＋y2＞0 |
| B．x1＋x2＜0，y1＋y2＞0 |
| C．x1＋x2＞0，y1＋y2＜0 |
| D．x1＋x2＜0，y1＋y2＜0 |