如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量
m=6.64×10-27kg,电荷量q =+3.2×10-19C,初速度
v = 3.2×106m/s。不计粒子重力(sin37°= 0.6,
cos37°= 0.8)求: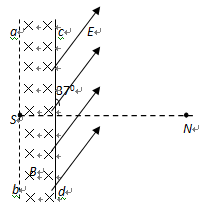
(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子,速度方向不变穿出金箔进入电场。在电场中运动通过N点,SN⊥ab且SN = 40cm,则此α粒子从金箔上穿出时的速度大小为多少?
如图所示,离地面足够高处有一竖直的空管,质量为2kg,管长为24m,M、N为空管的上、下两端,空管受到F=16N竖直向上的拉力作用,由静止开始竖直向下做加速运动,同时在M处一个大小不计的小球沿管的轴线以初速度v0竖直上抛,不计一切阻力,取g=10m/s2.求: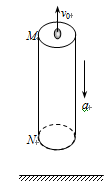
空管的加速度的大小与方向
若小球上抛的初速度为10m/s,经过多长时间从管的N端穿出?
若此空管的N端距离地面64m高,欲使在空管到达地面时小球必须落到管内,在其他条件不变的前提下,求小球的初速度v0大小的范围.
一个底面粗糙、质量为M的劈放在粗糙的水平面上,劈的斜面光滑且与水平面成30°角;现用一端固定的轻绳系一质量为m的小球,小球放在斜面上,小球静止时轻绳与竖直方向的夹角也为30°,如图所示,求: 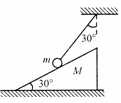
当劈静止时绳子的拉力大小.
地面对劈的摩擦力的大小和方向
若地面对劈的最大静摩擦力等于地面对劈支持力的k倍,为使整个系统静止,k值必满足什么条件?
如图所示,用半径为R=0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽,滚轮转动的角速度恒为ω=5rad/s,薄铁板的长为L=2.8m、质量为m=10kg,滚轮与铁板、铁板与工作台面间的动摩擦因数分别为μ1=0.3和μ2=0.1,铁板从一端放入工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力,其大小为F=100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽,g取10m/s2。
通过分析计算,说明铁板将如何运动;
加工一块铁板需要多少时间;
加工一块铁板电动机要多消耗多少电能。
如图所示,ABCDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的 圆周轨道,CDO是直径为15m的半圆轨道。AB轨道和CDO轨道通过极短的水平轨道(长度忽略不计)平滑连接。半径OA处于水平位置,直径OC处于竖直位置。一个小球P从A点的正上方高H处自由落下,从A点进入竖直平面内的轨道运动(小球经过A点时无机械能损失)。当小球通过CDO轨道最低点C时对轨道的压力等于其重力的
圆周轨道,CDO是直径为15m的半圆轨道。AB轨道和CDO轨道通过极短的水平轨道(长度忽略不计)平滑连接。半径OA处于水平位置,直径OC处于竖直位置。一个小球P从A点的正上方高H处自由落下,从A点进入竖直平面内的轨道运动(小球经过A点时无机械能损失)。当小球通过CDO轨道最低点C时对轨道的压力等于其重力的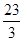 倍,取g为10m/s2。
倍,取g为10m/s2。
试求高度H的大小;
试讨论此球能否到达CDO轨道的最高点O,并说明理由;
求小球沿轨道运动脱离轨道后第一次落回轨道上时的速度大小。
完整的撑杆跳高过程可以简化成如图所示的三个阶段:持杆助跑、撑杆起跳上升、越杆下落。在第二十九届北京奥运会比赛中,俄罗斯女运动员伊辛巴耶娃以5.05m的成绩打破世界纪录。设伊辛巴耶娃从静止开始以加速度a=1.25m/s2匀加速助跑,速度达到v=9.0m/s时撑杆起跳,到达最高点时过杆的速度不计,过杆后做自由落体运动,重心下降h=4.05m时身体接触软垫,从接触软垫到速度减为零的时间t=0.90s。已知伊辛巴耶娃的质量m=65kg,重力加速度g取10 m/s2,不计空气的阻力。求:
伊辛巴耶娃起跳前的助跑距离;
假设伊辛巴耶娃从接触软垫到速度减为零的过程中做匀减速运动,求软垫对她的作用力大小。