已知集合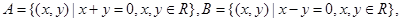 则集合
则集合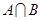 =( )
=( )
A.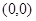 |
B.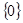 |
C.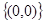 |
D.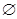 |
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每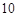 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②若两个变量的线性相关性越强,则相关系数的绝对值越接近于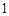 ;
;
③在某项测量中,测量结果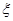 服从正态分布
服从正态分布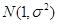
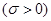 ,若
,若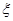 位于区域
位于区域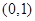 内的概率为
内的概率为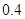 ,则
,则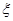 位于区域
位于区域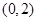 内的概率为
内的概率为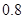 ;
;
④对分类变量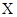 与
与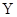 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“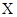 与
与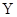 有关系”的把握越大.其中真命题的序号为()
有关系”的把握越大.其中真命题的序号为()
| A.①④ | B.②④ | C.①③ | D.②③ |
运行如图所示的程序框图,若输出的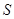 是
是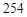 ,则①应为()
,则①应为()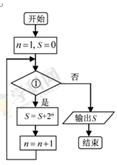
A.n≤5 |
B.n≤6 |
C.n≤7 |
D.n≤8 |
已知命题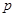 :函数
:函数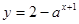 的图象恒过定点
的图象恒过定点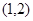 ;命题
;命题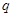 :若函数
:若函数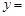
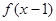 为偶函数,则函数
为偶函数,则函数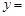
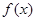 的图象关于直线
的图象关于直线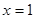 对称,则下列命题为真命题的是()
对称,则下列命题为真命题的是()
A.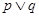 |
B.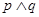 |
C.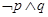 |
D.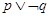 |
已知向量 ,
,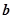
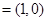 ,
,
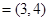 ,若
,若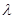 为实数,
为实数,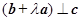 ,则
,则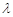 的值为()
的值为()
A. |
B.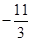 |
C. |
D. |
设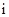 是虚数单位,则
是虚数单位,则 等于()
等于()
A. |
B. |
C. |
D. |