.(本小题满分16分)
已知椭圆
 上的一动点
上的一动点 到右焦点的最短距离为
到右焦点的最短距离为 ,且右焦点到右准线的距离等于短半轴的长.(1)求椭圆
,且右焦点到右准线的距离等于短半轴的长.(1)求椭圆 的方程;
的方程;
(2)设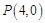 ,
,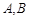 是椭圆
是椭圆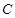 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结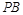 交椭圆
交椭圆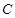 于另一点
于另一点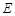 ,证明直线
,证明直线 与
与 轴相交于定点
轴相交于定点 ;
;
(3)在(2)的条件下,过点 的直线与椭圆
的直线与椭圆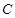 交于
交于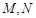 两点,求
两点,求 的取值
的取值
范围.
定义F(x,y)=(1+x)y,x,y∈(0,+∞).令函数f(x)=F(1,log2(x2-4x+9))的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O向曲线C1作切线,切点为B(n,t)(n>0),设曲线C1在点A,B之间的曲线段与线段OA,OB所围成图形的面积为S,求S的值.
求由抛物线y2=x-1与其在点(2,1),(2,-1)处的切线所围成的面积.
已知函数f(x)= x3-x2+ax-a(a∈R).
x3-x2+ax-a(a∈R).
(1)当a=-3时,求函数f(x)的极值.
(2)若函数f(x)的图象与x轴有且只有一个交点,求a的取值范围.
某工厂生产某种产品,每日的成本C(单位:元)与日产量x(单位:吨)满足函数关系式C=10000+20x,每日的销售额R(单位:元)与日产量x满足函数关系式R=
已知每日的利润y=R-C,且当x=30时,y=-100.
(1)求a的值.
(2)求当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
已知函数f(x)=x3-3x.
(1)求函数f(x)的单调区间.
(2)求函数f(x)在区间[-3,2]上的最值.