如图甲所示，两平行金属板AB间接有如图乙所示的电压，两板间的电场可看作匀强电场，且两板外无电场，板长L=0．8 m，板间距离d=0．6 m。在金属板右侧有一磁感应强度B=2．0×10-2 T，方向垂直纸面向外的匀强磁场，磁场宽度为l1=0．12 m，磁场足够长。MN为一竖直放置的足够大的荧光屏，荧光屏距磁场右边界的距离为l2=0．08 m，MN及磁场边界均与AB两板中线OO’垂直。现有带正电的粒子流由金属板左侧沿中线OO’连续射入电场中。已知每个粒子的速度v0=4．0×105 m/s，比荷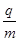
=1．0×108 C/kg，重力忽略不计，每个粒子通过电场区域的时间极短，电场可视为恒定不变。
(1)求t=0时刻进入电场的粒子打到荧光屏上时偏离O’点的距离； (2)试求能离开电场的粒子的最大速度，并通过计算判断该粒子能否打在右侧的荧光屏上。
如图所示，电阻
，小灯泡
上标有“3V，1．5W"，电源内阻
，滑动变阻器的最大阻值为R0（大小未知），当触头
滑动到最上端
时，安培表的读数为l A，小灯泡恰好正常发光，求：
滑动变阻器的最大阻值R0
当触头
滑动到最下端
时，求电源的总功率及输出功率。
如图所示，在方向水平的匀强电场中，一个不可伸长的不导电轻细线的一端连着一个质量为m的带电小球，另一端固定于O点，把小球拉直至细线与电场方向平行，然后无初速释放，已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ.求小球经过最低点时细线对小球的拉力.
一个带正电的质点，电量q=2.0×10-9库，在静电场中由a点移到b点，在这过程中，除电场力之外的其他力作功为6.0×10-5焦，质点的动能增加了8.0×10-5焦，则a、b两点间的电势差为多大?
如图所示，AB为一段光滑绝缘水平轨道，BCD为一段光滑的圆弧轨道，半径为R，今有一质量为m、带电荷量为＋q的绝缘小球，以速度
从A点向B点运动，后又沿弧BC做圆周运动，到C点后由于较小，故难运动到最高点．如果当其运动至C点时，忽然在轨道区域加一匀强电场和匀强磁场，此时轨道弹力为零，且贴着轨道做匀速圆周运动,使其能运动到最高点，，求：
匀强电场的方向和强度；
磁场的方向和磁感应强度．
小球到达轨道的末端点D后，将做什么运动？
如图所示，半径为r的圆形区域内存在着垂直纸面向里的匀强磁场，磁感应强度为B。现有一带电离子（不计重力）从A以速度v沿圆形区域的直径射入磁场，已知离子从C点射出磁场的方向间的夹角为60º
该离子带何种电荷；
求该离子的电荷量与质量之比q/m