如图,虚线下方有足够大的场强大小E=5.0×103 V/m和上方场强为8mg/3q的匀强电场,方向均水平向右。质量均为m=1.5×10-2kg的A、B小球,其中B球为绝缘小球且不带电,被长为R的绝缘丝线悬挂在O点刚好静止在虚线上, A球带电荷量为qA=+6.0×10-6C,在竖直平面内的以某一初速度v竖直进入电场,运动到B点速度刚好水平,同时与B球发生正碰并立即粘在一起围绕O点做半径为R=0.7m完整的圆周运动,假设甲、乙两球可视为质点,g取10 m/s2。(sin53°=0.8,c0s53°=0.6)
(1)假设初速度v="20m/s" ,试求小球A与B球碰撞前能运动的水平位移的大小和整个过程中电场力对小球做功的最大值。
(2)如果小球刚好能做完整的圆周运动,试求碰撞前A球的最小速度和绳子所受的最大拉力分别多大。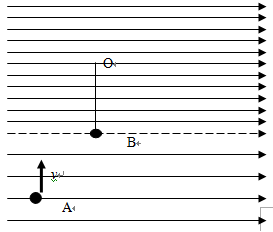
一个自由下落的物体,到达地面的速度是40 m/s.这个物体是从多高落下的?落到地面用了多长时间?(g=10m/s2)
如图所示,质量分别为M和m的物体用细线连接,悬挂在定滑轮上,定滑轮固定在天花板上,已知M>m,对滑轮及线的重量、摩擦不计,求细绳对天花板的拉力的大小?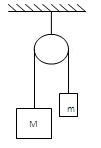
如图所示,一细线的一端固定于倾角为45°的光滑斜面体的顶端P处,细线的另一端拴一质量为m的小球。求:
(1)当斜面体至少以多大的加速度向左运动时,小球对斜面的压力为零?
(2)当斜面体以a=2g的加速度向左运动时,线中拉力为多大?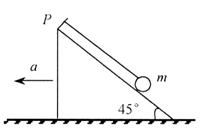
一质量m =40kg的小孩站在竖直电梯内的体重计上。电梯从t=0时刻由静止开始启动,在0到7s内体重计示数F的变化如图所示。试问:
(1)小孩乘电梯是上楼还是下楼?简述理由.
(2)在这段时间内电梯运动的距离是多少?(g=10m/s2)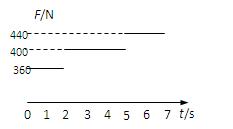
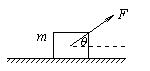
如图所示,质量为4 kg的物体静止于水平面上,物体与水平面间的动摩擦因数为0.5,物体受到大小为20N,与水平方向成37°角斜向上的拉力F作用时沿水平面做匀加速运动,
(1)求物体的加速度是多大?(g取10 m/s2)
(2)若10s后撤去拉力F,则物体总共运动多长位移。