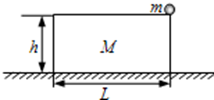如图所示,一质量为m、电荷量为+q、重力不计的带电粒子,从A板的S点由静止开始释放,经A、B加速电场加速后,穿过中间偏转电场,再进人右侧匀强磁场区域.已知AB间的电压为U,MN极板间的电压为2U,MN两板间的距离和板长均为L,磁场垂直纸面向里、磁感应强度为B、有理想边界.求:
(1) 带电粒子离幵B板时速度V0的大小;
(2) 带电粒子离开偏转电场时速度V的大小与方向;
(3) 要使带电粒子最终垂直磁场右边界射出磁场,磁场的宽度d多大?
一质量m=0.5kg的滑块以一定的初速度冲上一倾角为30º足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图为通过计算机绘制出的滑块上滑过程中的v-t图。g取10m/s2,求: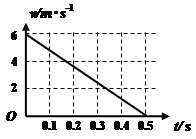
(1)滑块冲上斜面过程中的加速度大小;
(2)滑块与斜面间的动摩擦因数;
(3)判断滑块最后能否返回斜面底端?若能返回,求出返回斜面底端时的动能;若不能返回,求出滑块停在什么位置。
如图,质量M=8kg的小车放在光滑的水平面上,在小车左端加一水平力F="10" N,当小车向右运动的速度达到2. 5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数μ=0.3,小车足够长。g取10m/s2,求: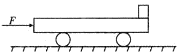
(1)小物块放上后,小物块及小车的加速度各为多大?
(2)经多长时间两者达到相同的速度?
(3)物体从放在小车上开始经t=1.5s通过的位移大小?
一质点在外力作用下沿直线做匀加速运动,从某时刻开始计时,测得该质点在第1 s内的位移为2.0 m,第5s内和第6s内的位移之和为11.2 m。求:
(1)该质点运动的加速度大小;
(2)该质点在第6s内的位移大小。
如图所示,两块相同平板P1,P2置于光滑水平面上,质量均为m。P2的右端固定一轻质弹簧,左端A与弹簧的自由端B相距L。物体P置于P1的最右端,质量为2m,且可看作质点。P1与P以共同速度v0向右运动,与静止的P2发生碰撞,碰撞时间极短。碰撞后P1与P2粘连在一起。P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内)。P与P2之间的动摩擦因数为μ。求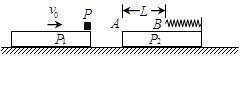
(1)P1、P2刚碰完时的共同速度v1和P的最终速度v2;
(2)此过程中弹簧的最大压缩量x和相应的弹性势能Ep。
如图,质量为M、长为L、高为h的矩形滑块置于水平地面上,滑块与地面间动摩擦因数为μ;滑块上表面光滑,其右端放置一个质量为m的小球。用水平外力击打滑块左端,使其在极短时间内获得向右的速度v0,经过一段时间后小球落地。求小球落地时距滑块左端的水平距离。