如图所示，一个质量为m=0.6kg的小球，在左侧平台上运行一段距离后从边缘A点以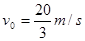
水平飞出，恰能沿切线从P点进入竖直圆弧管道并继续滑行。已知管道口径远小于圆弧半径，OP与竖直方向的夹角是37°，平台到地面的高度差为h=1.45m。若小球运动到圆弧轨道最低点时的速度大小是 10m/s。取g=10m/s2，sin53°=0.8，cos53°=0.6。求： 
(1)P点距地面的高度
(2)圆弧轨道最低点对小球支持力的大小
(3)若通过最高点Q点时小球对外管壁的压力大小9N，则小球经过Q点时的速度大小是多少？
如图7所示，光滑水平面右端B处连接一个竖直的半径为R的光滑半圆固定轨道，在离B距离为L的A点，用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力，质点沿半圆轨道运动到C处后又正好落回A点。求推力对小球所做的功。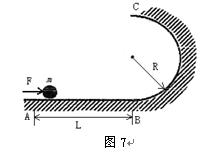
有一圆球形的天体，其自转周期为T(s)，在它两极处用弹簧秤称得某物体的重力为w(N)，在它的赤道处，称得该物体的重力w′=0.9w(N)，引力常量为G．则该天体的平均密度是多少?
10分）如图6所示，一根长0.1ｍ的细线，一端系着一个质量为0.18kg的小球，拉住线的另一端，使球在光滑的水平桌面上做匀速圆周运动。现使小球的转速很缓慢地增加，当小球的转速增加到开始时转速的3倍时，细线断开，线断开前的瞬间线的拉力比开始时大40N。求：(重力加速度ｇ=10m/s2)
（1）线断开前的瞬间，线的拉力大小。
（2）线断开的瞬间，小球运动的线速度大小。
（3）如果小球离开桌面时，速度方向与桌边的夹角为60°，桌面高出地面0.8m，求小球飞出后的落地点垂直到桌边的水平距离。
在光滑水平面上有一弹簧振子，弹簧的径度系数为k，振子质量为M，振动的最大速度为
0，如图6所示，当振
子在最大位移为A的时刻把质量为m的物体轻放其上，则
（1）要保持物体和振子一起振动，二者间最大静摩擦力至少是多少？
（2）一起振动时，二者过平衡位置的速度多大？
有一单摆，当摆线与竖直方向成
角（
50）时，摆球的速度为零，摆球运动到最低点时的速度为
，求此单摆的周期。