设m＝2100，n＝375，为了比较m与n的大小．小明想到了如下方法：m＝2100＝（24）25＝1625，即25个16相乘的积；n＝375＝（33）25＝2725，即25个27相乘的积，显然m＜n，现在设x＝430，y＝340，请你用小明的方法比较x与y的大小
解方程组：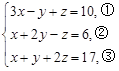
（1）先化简，再求值：(x＋2y)(x－2y)＋(x＋2y)2－4xy，其中x＝－1，y＝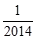
．
（2）已知两个单项式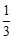
am＋2nb与－2a4bk是同类项，求：2m·4n·8k的值．
把下列各式进行因式分解：
（1）(x＋2)2y－y：（2）a2－2a(b＋c)＋(b＋c)2．
计算：（1）20－3－2＋(－2)3；
（2）(3m2)3＋(－2m3)2－m·m5．
已知如图1，线段AB、CD相交于点O，连结AC、BD，我们把形如图1的图形称之为“8字形”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥聪明才智，解决以下问题：
（1）在图1中，请写出∠A、∠B、∠C、∠D之间的数量关系，并说明理由；
（2）仔细观察，在图2中“8字形”的个数有个；
（3）在图2中，若∠B＝76°，∠C＝80°，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N利用（1）的结论，试求∠P的度数；
（4）在图3中，如果∠B和∠C为任意角，并且AP和DP分别是∠CAB和∠BDC的三等分线，即∠PAO＝
∠CAO， ∠BDP＝∠BOD，那么∠P与∠C、∠B之间存在的数量关系是（直接写出结论即可）．