劳伦斯和利文斯设计的回旋加速器工作原理如图所示，置于高真空中的D形金属半径为R，两盒间的狭缝很小，带电粒子穿过的时间可忽略，磁感应强度为B的匀强磁场与盒面垂直，高频交流电频率为f，加速电压为U.若A处粒子源产生的质子质量为m、电荷量为＋q，在加速器中被加速，且加速过程中不考虑相对论效应和重力的影响，则下列说法正确的是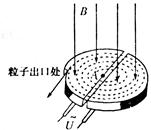
| A．质子被加速后的最大速度不可能超过2πRf |
| B．质子离开回旋加速器时的最大动能与加速电压U成正比 |
| C．质子离开回旋加速器时的最大动能与交流电频率f成正比 |
| D．质子第2次和第1次经过两D形盒间狭缝后轨道半径之比为1∶ |
图中为一理想变压器，其原线圈与一电压有效值不变的交流电源相连,P为滑动头。现令P从均匀密绕的副线圈最底端开始，沿副线圈匀速上滑，直至白炽灯L两端的电压等于其额定电压为止。用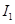
表示流过原线圈的电流，
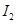表示流过灯泡的电流，
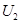表示灯泡两端的电压，
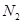表示灯泡消耗的电功率（这里的电流、电压均指有效值）。下列4个图中，能够正确反映相应物理量的变化趋势的是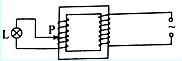
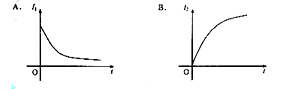
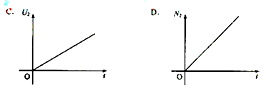
把一只电热器接到100 V的直流电源上，在t时间内产生的热量为Q，若将它分别接到U1="100sinωt" V和U2="50sin2ωt" V的交变电流电源上，仍要产生热量Q，则所需时间分别是
| A．t，2t | B．2t，8t | C．2t，2t | D．t， t |
一交流电压为u＝100
sin100πt V，由此表达式可知( )
| A．用电压表测该电压其示数为100 V |
| B．该交流电压的周期为0.02 s |
| C．将该电压加在100 Ω的电阻两端，电阻消耗的电功率为200 W |
| D．t＝1/400 s时，该交流电压的瞬时值为100 V |
矩形线圈绕垂直磁场线的轴匀速转动，对于线圈中产生的交变电流 ( )
| A．交变电流的周期等于线圈转动周期 |
| B．交变电流的频率等于线圈的转速 |
| C．线圈每次通过中性面，交变电流改变一次方向 |
| D．线圈每次通过中性面，交变电流达到最大值 |
下列有关气体分子动理论的说法中正确的是（）
| A．对大量分子整体统计，气体分子的运动是有规律的 |
| B．温度升高时每个气体分子的速率都将增大，因此气体分子的平均速率也将增大 |
| C．在一定温度下，某种气体的分子速率分布是确定的 |
| D．气体的压强只跟气体的温度有关，温度越高压强越大 |