如图，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．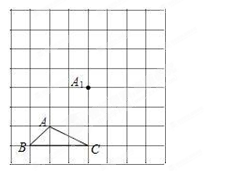
（1）把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；
（2）把△A1B1C1绕点A1按逆时针方向旋转90°，在网格中画出旋转后的△A1B2C2；
（3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．
若
，求
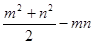的值
（1、3小题各4分，2、4小题各5分，共18分）因式分解：
（1）
(2) a2－b2＋2b－1
（3）x2－10x＋25；（4）
解下列不等式（组），并把不等式的解集表示在数轴上。（每小题5分，共10分）
（1）1＋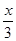
＞5－
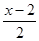（2）
（本大题12分）某镇组织10辆汽车装运完A、B、C三种不同品质的湘莲共100吨到外地销售，按计划10辆汽车都要装满，且每辆汽车只能装同一种湘莲，根据下表提供的信息，解答以下问题：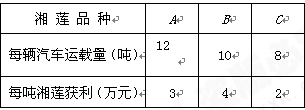
（1）设装运A种湘莲的车辆数为x，装运B种湘莲的车辆数为y，求y与x之间的函数关系式；
（2）如果装运每种湘莲的车辆数都不少于2辆，那么车辆的安排方案有几种？并写出每种安排方案；
（3）在（2）的方案中，若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值.
（本大题12分）反比例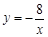函数
与一次函数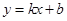
的图象交于A（
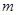，4）、
B（4,
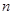）两点．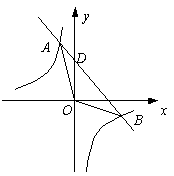
（1）求A、B两点的坐标；
（2）求一次函数解析式；
（3）求△AOB的面积；
（4）当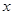
为何值时，反比例函数的值大于一次函数的值？(直接写出结果)