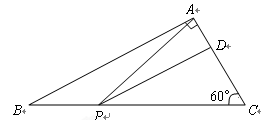
如图,在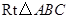 中,
中, 点
点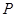 是
是 边上的动点(点
边上的动点(点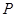 与点
与点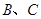 不重合),过动点
不重合),过动点 作
作 交
交 于点
于点
(1)若 与
与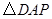 相似,则
相似,则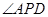 是多少度?
是多少度?
(2)试问:当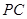 等于多少时,
等于多少时, 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(3)若以线段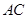 为直径的圆和以线段
为直径的圆和以线段 为直径的圆相外切,
为直径的圆相外切,
求线段 的长.
的长.
若解关于x的分式方程 会产生增根,求m的值。
会产生增根,求m的值。
先化简,再求值: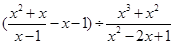 ,其中x为不等式组
,其中x为不等式组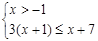 的整数解.
的整数解.
解方程: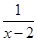
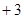 =
=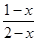
RtΔABC中,∠C=90°,点D、E分别是ΔABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠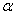 .
.
(1)若点P在线段AB上,如图(1)所示,且∠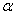 =50°,则∠1+∠2=___________°;
=50°,则∠1+∠2=___________°;
(2)若点P在边AB上运动,如图(2)所示,则∠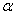 、∠1、∠2之间有何关系?
、∠1、∠2之间有何关系?
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠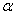 、∠1、∠2之间有何关系?猜想并说明理由。
、∠1、∠2之间有何关系?猜想并说明理由。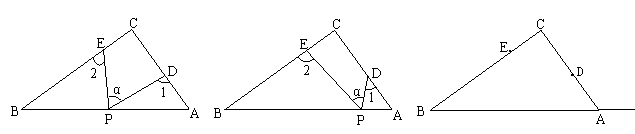
已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。