桌生产厂家研究发现，倾斜12°～24°的桌面有利于学生保持躯体自然姿势．根据这一研究，厂家决定将水平桌面做成可调节角度的桌面．新桌面的设计图如图1，AB可绕点A旋转，在点C处安装一根可旋转的支撑臂CD，AC＝30cm．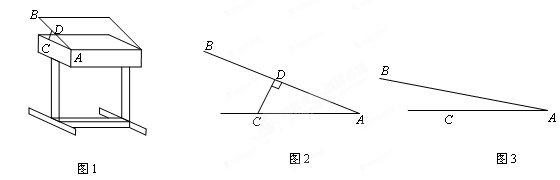 
（1）如图2，当∠BAC＝24°时，CD⊥AB，求支撑臂CD的长；
（2）如图3，在 (1)中 CD的长不变的情况下，当∠BAC＝12°时，求AD的长．（结果保留根号）
（参考数据： sin24°≈0.40，cos24°≈0.91，tan24°≈0.46， sin12°≈0.20）
已知二次函数
．
（1）求该函数图象的顶点坐标．
（2）求此抛物线与
轴的交点坐标．
已知a ：b ：c="2" ：3 ：4，且2a＋3b－2c=10，求a， b，c的值。
如图，已知：∠ACB =∠ADC=90°，AD=2，CD=
,当AB的长为_____________时，△ACB与△ADC相似．
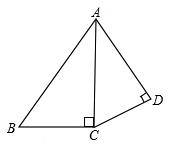
有一长为240米的圆形跑道，小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步．已知小明的速度为4米/秒，小狗的速度为12米/秒．跑步的时间记为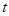
秒．在跑步过程中，小明和他的小狗之间相距（取两者之间较短一段圆弧跑道的长度）为
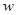米．
（1）当
秒和
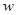秒时，分别求的值？
（2）当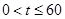
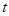时，请用含的代数式表示．
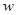（3）当
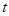时，请用含的代数式表示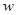．（可直接写出结果）
某空调器销售商，今年四月份销出空调
台，五月份销售空调比四月份的2倍多1台，六月份销售空调比前两个月的总和的4倍少15台．
（1）用代数式表示该销售商今年第二季度共销售空调多少台？
（2）当四月份销出空调为111台时，求第二季度销售的空调总数．