两绳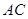 和
和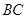 同时系一质量为
同时系一质量为 的小球,且
的小球,且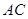 绳长为
绳长为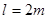 ,两绳都拉直时与竖直方向的夹角分别为
,两绳都拉直时与竖直方向的夹角分别为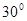 角和
角和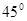 角,如图4所示。当小球以
角,如图4所示。当小球以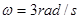 绕
绕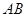 为轴转动时,上、下两绳的拉力分别是多少?
为轴转动时,上、下两绳的拉力分别是多少?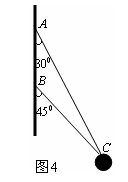
如图为一质点在0s到22s内做直线运动的速度-时间图像,试求: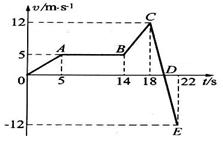
(1)OA过程与BC过程加速度大小之比为多少?
(2)质点做匀减速运动的位移大小是多少?
(3)质点在前10s内的平均速度是多少?
2012年9月25日,我国第一艘航空母舰“辽宁号”正式服役,这是我国军事上的一件大事。假如某一艘航空母舰上装有帮助飞机起飞的弹射系统,已知某型号的战斗机在跑道上加速时可产生的最大加速度为5.0 m/s2,起飞速度为50m/s,假设航母静止不动,问:
(1)如果航母上不安装弹射系统,要求这种飞机仍能在舰上起飞,问甲板上跑道至少为多长?
(2)如果航母弹射系统给飞机一个30m/s的初速度,则飞机在跑道上至少要加速多长时间才能起飞?
一个电视显像管的电子束里电子的动能EK=12000eV.这个显像管的位置取向刚好使电子水平地由南向北运动.已知地磁场的竖直向下分量B=5. 5×10-5T,试问(1)电子束偏向什么方向? (2)电子束在显像管里由南向北通过y=20cm路程,受洛仑兹力作用将偏转多少距离(结果保留一位有效数字)?电子质量m=9.1×10-31kg,电量e=1.6×10-19C.
如图12所示,一个半径为R的绝缘光滑半圆环,竖直放在场强为E的匀强电场中,电场方向竖直向下.在环壁边缘处有一质量为m,带有正电荷q的小球,由静止开始下滑,求小球经过最低点时对环底的压力.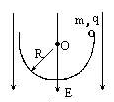
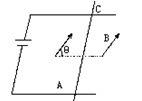
如图所示,通电导体棒AC静止于水平导轨上,棒的质量为m长为L,通过的电流强度为I,匀强磁场的磁感强度B的方向与导轨平面成θ角,求导轨受到AC棒的压力和摩擦力各为多大?