如图所示，一半径R＝0．2m的水平圆盘绕过圆心的竖直轴转动，圆盘边缘有一质量m＝1．0kg的小滑块。当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，经光滑的过渡圆管（图中圆管未画出）进入轨道ABC。已知AB段为光滑的弧形轨道，A点离B点所在水平面的高度h＝1．2m；BC斜面与AB轨道对接，倾角为37°，滑块与圆盘及BC斜面间的动摩擦因数均μ＝0．5，滑块在运动过程中始终未脱离轨道，不计在过渡圆管处和B点的机械能损失，最大静摩擦力近似等于滑动摩擦力，取g＝10m／s2，sin37°＝0．6，cos37°＝0．8
（1）当圆盘的角速度多大时，滑块从圆盘上滑落?
（2）若取圆盘所在平面为零势能面，求滑块到达B点时的机械能。
（3）从滑块到达B点时起，经0．6s正好通过C点，求BC之间的距离。
如图所示，在质量为M的试管内盛有少量乙醚，管口用质量为m的软木塞封闭，加热试管，软木塞在乙醚蒸汽的压力作用下飞出后，恰能使试管绕悬挂点在竖直平面内做一完整的圆周运动. 求：（1）若试管系于长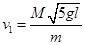
的轻质细线上，则软木塞飞出的速度至少为多大？（2）若试管系于长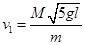的轻质细杆上，则软木塞飞出的速度至少为多大？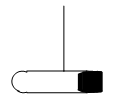
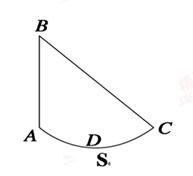
一玻璃砖横截面如图所示，其中ABC为直角三角形(AC边未画出)，AB为直角边，∠ABC＝45°；ADC为一圆弧，其圆心在BC边的中点．此玻璃的折射率为2 .点光源S在圆心正下方，并且S到圆心的距离为2m， BC=2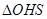
m，若S发出的光线只有三条从AB边射出去的是水平的，求这三条水平光线中相邻的光线间的距离。（不考虑多次反射）（sin750=
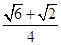,cos750=
）
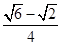如图所示，电量为q=2×10-8C，质量为m=2×10-10kg的带正电的粒子从M 点以与MN方向成1200角出发，同时有一长为L的薄板从M点由静止开始做加速度为a=0.2m/s2的匀加速运动。薄板为半透板，当粒子从上向下和板相遇时，粒子会穿过薄板，不受影响。从下向上和薄板相遇会发生碰撞，粒子每次和薄板碰撞用时极短，电量不变，和薄板垂直速度大小不变，方向相反，和薄板平行速度不变。匀强磁场垂直纸面向里，大小B=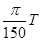
。MN的长度6m，粒子从M出发经过9s恰好到N。不计重 。求：
（1）粒子出发以后第一次和薄板相撞所需要的时间；
（2）粒子的速度；
（3）薄板的最小长度。
有可视为质点的木块由A点以一定的初速度为4m/s水平向右运动，AB的长度为2m,物体和AB间动摩擦因素为μ1=0.1，BC无限长，物体和BC间动摩擦因素为μ2=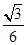
， 求：
（1）物体第一次到达B点的速度
（2）通过计算说明最后停在水平面上的位置
两物块A、B用轻弹簧相连，质量均为2 kg，初始时弹簧处于原长，A、B两物块都以v＝6m／s的速度在光滑的水平地面上运动，质量4 kg的物块C静止在前方，如图所示。B与C碰撞后二者会粘在一起运动。求在以后的运动中：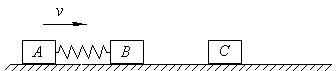
（1）B与C碰撞后瞬间，物块B的速度为多大?
（2）当弹簧的弹性势能最大时，物块A的速度为多大?
（3）系统中弹性势能的最大值是多少?