如图均匀薄壁U形管，左管上端封闭，右管开口且足够长，管的截面积为S，内装有密度为ρ的液体。右管内有一质量为m的活塞搁在固定卡口上，卡口与左管上端等高，活塞与管壁间无摩擦且不漏气。温度为T0时，左、右管内液面等高，两管内空气柱长度均为L，压强均为大气压强P0，重力加速度为g。现使左右两管温度同时缓慢升高，在活塞离开卡口上升前，左右两管液面保持不动，试求：
（1）温度升高到T1为多少时，右管活塞开始离开卡口上升；
（2）温度升高到T2为多少时，两管液面高度差为L。
弹簧振子以O点为平衡位置在B．C两点间做简谐振动，在t=0时刻，振子从O．B间的P点以速度v向B点运动；在t=0.20s时，振子速度第一次变为―v；在t=0.50s时，振子速度第二次变为―v。
(1)求弹簧振子的振动周期T。
(2)若B．C之间的距离为25cm，求振子在4.00s内通过的路程。
(3)若B．C之间的距离为25 cm，从平衡位置计时，写出弹簧振子位移的表达式，并画出弹簧振子的振动图象。
如图所示，在以坐标原点O为圆心．半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t0时间从P点射出。
（1）求电场强度的大小和方向。
（2）若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
（3）若仅撤去电场，带电粒子仍从O点射入，且速度为原来的4倍，
求粒子在磁场中运动的时间。
如图所示，一透明半圆柱体折射率为n=2，底面半径为R．长为L。一平行光束从半圆柱体的矩形表面垂直射入，从部分柱面有光线射出。求该部分柱面的面积S。
如图所示，摩托车做特技表演时，以v0=10.0m/s的初速度冲向高台，然后从高台水平飞出。若摩托车冲向高台的过程以P=4.0kw的额定功率行驶，冲到高台上所用时间t=3.0s，人和车的总质量
kg，台高h=5.0m，摩托车的落地点到高台的水平距离x=10.0m。不计空气阻力，取
。求：
(1)摩托车从高台飞出到落地所用时间；
(2)摩托车落地时速度的大小；
(3)摩托车冲上高台过程中克服阻力所做的功。
如图所示，半径R="2" m 的四分之一粗糙圆弧轨道AB置于竖直平面内，轨道的B端切线水平，且距水平地面高度为h="1.25" m，现将一质量m="0.2" kg 的小滑块从A点由静止释放，滑块沿圆弧轨道运动至B点以
的速度水平飞出（g取10 m/s2）．求：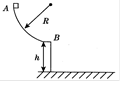
（1）小滑块经过B点时对圆轨道的压力大小；
（2）小滑块着地时的速度大小和方向．