如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B。电阻为R、半径为L、圆心角为45°的扇形闭合导线框绕垂直于纸面的O轴以角速度ω匀速转动(O轴位于磁场边界)。则线框内产生的感应电流的有效值为( )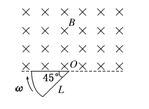
A. B.
C. D.
“嫦娥二号”是我国月球探测第二期工程的先导星。若测得“嫦娥二号”在月球(可视为密度均匀的球体)表面附近圆形轨道运行的周期T,已知引力常量为G,半径为R的球体体积公式 ,则可估算月球的()
,则可估算月球的()
| A.密度 | B.质量 | C.半径 | D.自转周期 |
一行星绕恒星作圆周运动。由天文观测可得,其运动周期为T,速度为v,引力常量为G,则()
A.恒星的质量为 |
B.行星的质量为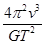 |
C.行星运动的轨道半径为 |
D.行星运动的加速度为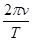 |
2009年5月,航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示,关于航天飞机的运动,下列说法中正确的有( )
| A.在轨道Ⅱ上经过A的速度小于经过B的速度 |
| B.在轨道Ⅱ上经过A的动能小于在轨道Ⅰ上经过A的动能 |
| C.在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期 |
| D.在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度 |
为了对火星及其周围的空间环境进行探测,我国预计于2011年10月发射第一颗火星探测器“萤火一号”.假设探测器在离火星表面高度分别为h1和h2的圆轨道上运动时,周期分别为T1和T2.火星可视为质量分布均匀的球体,且忽略火星的自转影响,万有引力常量为G.仅利用以上数据,可以计算出( )
| A.火星的密度和火星表面的重力加速度 |
| B.火星的质量和火星对“萤火一号”的引力 |
| C.火星的半径和“萤火一号”的质量 |
| D.火星表面的重力加速度和火星对“萤火一号”的引力 |
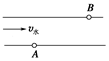
一条自西向东的河流,南北两岸分别有两个码头A、B,如图所示.已知河宽为80 m,河水水流的速度为5 m/s,两个码头A、B沿水流的方向相距100 m.现有一种船,它在静水中的行驶速度为4 m/s,若使用这种船渡河,且沿直线运动,则
( )
A.它可以正常来往于A、B两个码头
B.它只能从A驶向B,无法返回
C.它只能从B驶向A,无法返回
D.无法判断