匝数为N、面积为S、总电阻为R的矩形闭合线圈,在磁感应强度为B的匀强磁场中按如图所示方向(俯视逆时针)以角速度ω绕轴 匀速转动。t=0时线圈平面与磁感应线垂直,规定adcba的方向为电流的正方向,求:
匀速转动。t=0时线圈平面与磁感应线垂直,规定adcba的方向为电流的正方向,求:
(1)线圈转动过程中感应电动势瞬时值的表达式;
(2)线圈转到与图示位置成 角时的瞬时电流;
角时的瞬时电流;
(3)线圈转动一周过程中外力做的功。
如图所示的电路中,电源由6个电动势E0="1.5" V、内电阻r0="0.1" Ω的电池串联而成;定值电阻R1="4.4" Ω,R2="6" Ω,R2允许消耗的最大电功率为Pm="3.375" W,变阻器开始接入电路中的电阻R3="12" Ω,求: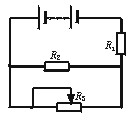
(1)开始时通过电池的电流多大?电源的输出功率多大?
(2)要使R2实际消耗的功率不超过允许的最大值,可变电阻R3的取值范围是什么?
如图所示,分别在A、B两点放置点电荷 和
和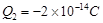 ,在AB的垂直平分线上有一点C,且
,在AB的垂直平分线上有一点C,且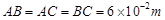 。(静电力常量k=
。(静电力常量k=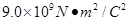 )试求:
)试求: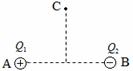
(1)C点的电场强度的大小和方向。
(2)如果有一电子静止在C点,它所受的库仑力的大小和方向。
如图所示,一块小磁铁放在铁板ABC的A处,其中AB长x1=1m,BC长x2=0.5m,BC与水平面间的夹角为37°,小磁铁与铁板间的引力为磁铁重的0.2倍,小磁铁与铁板间的动摩擦因数μ=0.25,现在给小磁铁一个水平向左的初速度v0=4m/s。小磁铁经过B处时速率不变(sin37°=0.6,cos37°=0.8)g取10m/ ,求:
,求:
(1)小磁铁第一次到达B处的速度大小;
(2)小磁铁在BC段向上运动时的加速度大小;
(3)请分析判断小磁铁能否第二次到
达B处。
如图所示,物体A的质量m=4kg,小车B的质量M=5kg,叠放在光滑水平面上,在A上施加一水平力 =20N时,A,B恰好能发生相对滑动,若不施加
=20N时,A,B恰好能发生相对滑动,若不施加 ,而对B施加一水平拉力,求:若要保持A,B间相对静止,对B物体施加的最大水平拉力为多大?(g取10m/
,而对B施加一水平拉力,求:若要保持A,B间相对静止,对B物体施加的最大水平拉力为多大?(g取10m/ )
)
如图所示,一小物体所受的重力为100N,用细线AC、BC和轻弹簧吊起,处于平衡状态。已知弹簧原长为1.5cm, 劲度系数k=8000N/m, 细线AC长为4cm, ∠BAC=300,∠CBA=600,求细线AC、BC对小物体的拉力各是多少?