(10分）如图，CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且AO平分∠BAC。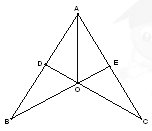
（1）求证：△ADO≌△AEO
（2）猜想OB与OC的数量关系，并说明理由.
如图，方格纸中的每个小方格都是边长为1的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，A（－1，5），B（－1，0），C（－4，3）．
（1）画出△ABC关于y轴对称的△A1B1C1；（其中A1、B1、C1是A、B、C的对应点，不写画法）
（2）写出A1、B1、C1的坐标；
（3）求出△A1B1C1的面积．
一种蔬菜
千克，不加工直接出售每千克可卖
元；如果经过加工质量减少了20%，价格增加了40%，问：
（1）千克这种蔬菜加工后可卖多少钱？
（2）如果这种蔬菜1 000千克，不加工直接出售每千克可卖1.50元，问加工后原1 000千克这种蔬菜可卖多少钱？比加工前多卖多少钱？
已知
，先化简再求
的值．
按要求作图：如图，在同一平面内有四个点A、B、C、D．
①画射线CD；②画直线AD；③连结AB；④直线BD与直线AC相交于点O．
已知A=
，B=
．且3A+6B的值与x无关，求y的值．