(本题12分) 如果一个正整数能够表示为两个连续的偶数的平方差,那么称这个正整数为“神秘数”.如4=22－02；12=42－22；20=62－42.因此4、12、20这三个数都是神秘数.
(1)请你写出50以内的两个神秘数（除4、12、20外），并判断2012是否是神秘数？（不要说明理由）
(2)设两个连续偶数为2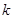
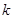+2和2 (其中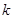为非负整数)，由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
(3)试说明：两个连续奇数的平方差(取正数)不是神秘数.
如图，点A、B、C、D为⊙O的四等分点，动点P从圆心O出发，沿线段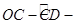
线段DO的路线作匀速运动．设运动时间为
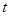秒,∠APB的度数为
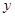度，则下列图象中表示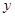与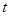的函数关系最恰当的是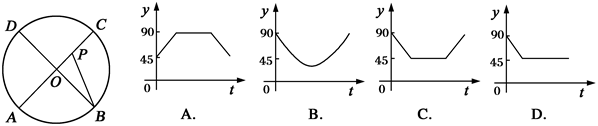
已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，给出以下结论：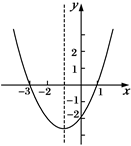
①因为a＞0，所以函数
有最大值；
②该函数图象关于直线
对称；
③当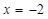
时，函数y的值大于0；
④当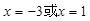
时，函数y的值都等于0．
其中正确结论的个数是
| A．1 | B．2 | C．3 | D．4 |
如图，在△ABC中，DE∥BC，AD =2DB，△ABC的面积为36，则△ADE的面积为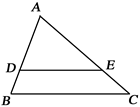
| A．81 | B．54 |
| C．24 | D．16 |
将抛物线
向右平移2个单位后得到新的抛物线，则新抛物线的解析式是
A． |
B． |
C． |
D． |
已知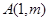点
与点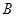
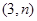都在反比例函数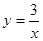
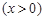的图象上，则m与n的关系是
A． |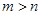
B． |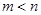
C． |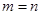
D．不能确定 |