某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析，画出频率分布直方图（如右图）．记成绩不低于90分者为“成绩优秀”．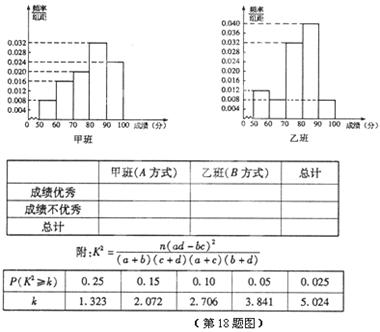
（I）从乙班随机抽取2名学生的成绩，记“成绩优秀”的个数为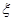
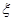，求的分布列和数学期望；
（II）根据频率分布直方图填写下面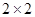
列联表，并判断是否有95%的把握认为“成绩优秀”与教学方式有关。
如下图所示，求△PQR内任一点(x,y)满足的关系式.
求z=3x+5y的最大值和最小值,使式中的x、y满足约束条件
已知
、
是两个不共线的向量，若它们起点相同，
、
、t（+）三向量的终点在一直线上，则实数t=_________.
已知平行四边形ABCD的两条对角线AC与BD交于E，O是任意一点，
求证：
+
+
+
=4
判断下列命题是否正确，若不正确，请简述理由.
①向量
与
是共线向量，则A、B、C、D四点必在一直线上；
②单位向量都相等；
③任一向量与它的相反向量不相等；
④四边形ABCD是平行四边形的充要条件是＝
⑤模为0是一个向量方向不确定的充要条件；
⑥共线的向量，若起点不同，则终点一定不同.