如图,抛物线与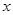 轴交于
轴交于 (
(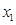 ,0)、
,0)、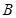 (
(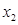 ,0)两点,且
,0)两点,且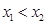 ,与
,与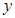 轴交于点
轴交于点 ,其中
,其中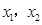 是方程
是方程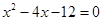 的两个根。
的两个根。
(1)求抛物线的解析式; (2)点
(2)点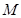 是线段
是线段 上的一个动点,过点
上的一个动点,过点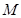 作
作 ∥
∥ ,交
,交 于点
于点 ,连接
,连接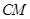 ,当
,当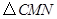 的面积最大时,求点
的面积最大时,求点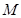 的坐标;
的坐标;
(3)点 在(1)中抛物线上,
在(1)中抛物线上,
点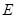 为抛物线上一动点,在
为抛物线上一动点,在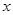 轴上是
轴上是
否存在点 ,使以
,使以 为顶
为顶
点的四边形是平行四边形,如果存在,
求出所有满足条件的点 的坐标,
的坐标,
若不存在,请说明理由。
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是()
| A.800 | B.600 | C.400 | D.200 |
如图,EF∥BC,AC平分∠BAF,∠B=50°,则∠C的度数是()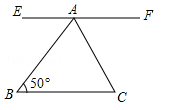
| A.50° | B.55° | C.60° | D.65° |
下列说法正确的是()
| A.掷一枚硬币,正面一定朝上 |
| B.某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖 |
| C.旅客上飞机前的安检应采用抽样调查 |
| D.方差越大,数据的波动越大 |
视力表的一部分如图,其中开口向上的两个“E”之间的变换是()
| A.平移 | B.旋转 | C.对称 | D.位似 |
若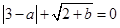 ,则
,则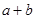 的值是()
的值是()
| A.2 | B.1 | C.0 | D.﹣1 |