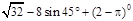小王家是新农村建设中涌现出的“养殖专业户”．他准备购置80只相同规格的网箱，养殖A、B两种淡水鱼（两种鱼不能混养）．计划用于养鱼的总投资不少于7万元，但不超过7.2万元，其中购置网箱等基础建设需要1.2万元．设他用x只网箱养殖A种淡水鱼，目前平均每只网箱养殖A、B两种淡水鱼所需投入及产业情况如下表：
| 项目类别 |
鱼苗投资 （百元） |
饲料支出 （百元） |
收获成品鱼（千克） |
成品鱼价格 （百元/千克） |
| A种鱼 |
2.3 |
3 |
100 |
0.1 |
| B种鱼 |
4 |
5.5 |
55 |
0.4 |
（1）小王有哪几种养殖方式？
（2）哪种养殖方案获得的利润最大？
（3）根据市场调查分析，当他的鱼上市时，两种鱼的价格会有所变化，A种鱼价格上涨a%（0＜a＜50），B种鱼价格下降20%，考虑市场变化，哪种方案获得的利润最大？（利润=收入-支出．收入指成品鱼收益，支出包括基础建设投入、鱼苗投资及饲料支出）
从“中国环境保护部数据中心”获得某市环保监测站提供的资料，从中随机抽取
了今年1~3月份中的30天的空气污染指数（API）如下：
64, 100, 61, 60, 59, 108, 78, 63, 101, 63, 69, 69, 104, 72, 45, 54, 75, 57, 78, 87, 124, 115, 98, 87, 78, 86, 106, 70, 79, 73.
空气质量级别表
| 空气污染 指数 |
0～50 |
51～100 |
101～150 |
151～200 |
201～250 |
251～300 |
300以上 |
| 空气质量 级别 |
I级 |
Ⅱ级 |
Ⅲ（1）级 |
Ⅲ（2）级 |
Ⅳ（1）级 |
Ⅳ（1）级 |
Ⅴ级 |
| 空气质量 状况 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中度重 污染 |
重度 污染 |
请你根据空气质量级别表和上述空气污染指数，解答以下问题：
（1）填写频率分布表中未完成的空格；
| 分组 |
频数统计 |
频数 |
频率 |
| 0~50 |
 |
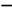1 |
0.03 |
| 51~100 |
 |
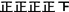23 |
① |
| 101~150 |
 |
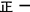6 |
② |
| 合计 |
30 |
30 |
1.00 |
（2）写出统计数据中的中位数、众数；
（3）利用以上信息，试估计该市今年（按360天计算）空气质量是优良（包括Ⅰ、Ⅱ级）的天数．
如图．在△ABC中．D是AB的中点．E是CD的中点．过点C作CF∥AB交AE的延长线于点F．连结BF。
（1）求证：DB=CF；
（2）在△ABC中添加一个条件：，使四边形BDCF为（填：矩形或菱形）。
如图，点B的坐标为（4，3），过点B作x轴的垂线垂足为A，交反比例函数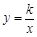
(x>0)图象于点C；连结OB交反比例函数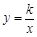(x>0) 图象于点D，已知BC∶AB=2∶3。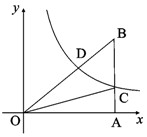
（1）求k的值
（2）求点D的坐标。
解方程：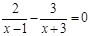
．
计算：