如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b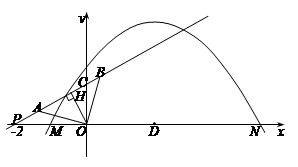
与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=
，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．
(1)OH的长度等于___________；k＝___________，b＝____________；
(2)是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶
点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜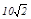
，写出探索过程．
如图，AB∥ED，∠ECF＝70°，则∠BAF的度数为（ ）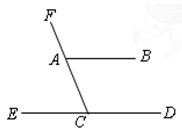
| A．130° | B．110° | C．70° | D．20° |
下列图形中不是中心对称图形的是（ ）
| A．矩形 | B．菱形 | C．正五边形 | D．平行四边形 |
下列运算正确的是（ ）
| A．3a＋2a＝5a2 | B．(2a)3＝6a3 |
| C．(x＋1)2＝x2＋1 | D．x2－4＝(x＋2)(x－2) |
－3的绝对值是（ ）
| A．3 | B．－3 | C． |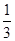
D．－ |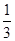
如图，已知抛物线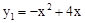
和直线
.我们约定：当x任取一值时，x对应的函数值分别为y1、y2，若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2.下列判断：①当x＞2时，M=y2；②当x＜0时，x值越大，M值越大；③使得M大于4的x值不存在；④若M=2，则x=1.其中正确的有（）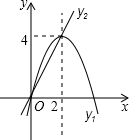
| A．1个 | B．2个 | C．3个 | D．4个 |