如图所示的螺线管的匝数n=1500,横截面积S=20cm2,电阻r=1.5Ω,与螺线管串联的外电阻R1=10Ω,R2=3.5Ω。若穿过螺线管的磁场的磁感应强度按图(b)所示的规律变化
求(1)螺线管两端M、N间的电压。
(2)R1上消耗的电功率。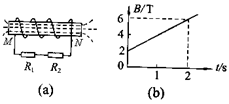
如图所示,竖直放置的半圆形光滑绝缘轨道半径为R,圆心为O,最高点为D,下端与绝缘水平轨道在B点平滑连接。一质量为m、带电量为+q的小物块置于水平轨道上的A点。已知A、B两点间的距离为L,小物块与水平轨道间的动摩擦因数为μ,重力加速度为g。
(1)若物块能到达的最高点是半圆形轨道上与圆心O等高的C点,则物块在A点水平向左的初速度应为多大?
(2)若整个装置处于方向竖直向上的匀强电场中,物块在A点水平向左的初速度vA=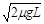 ,沿轨道恰好能到达最高点D,并向右飞出,则匀强电场的场强E多大?
,沿轨道恰好能到达最高点D,并向右飞出,则匀强电场的场强E多大?
(3)若整个装置处于方向水平向左、场强大小E′= 的匀强电场中,现将物块从A点由静止释放,
的匀强电场中,现将物块从A点由静止释放,
运动过程中始终不脱离轨道,求物块第2n(n=1、2、3……)次经过B点时的速度大小。
篮球比赛时,为了避免对方运动员的拦截,往往采取将篮球与地面发生一次碰撞后传递给队友的方法传球——击地传球。设运动员甲以v0=5m/s 的水平速度将球从离地面高 h1=0.8m处抛出,球与地面碰撞后水平方向的速度变为原来水平速度的4/5,竖直方向离开地面瞬间的速度变为与地面碰前瞬间竖直方向速度的3/4,运动员乙恰好在篮球的速度变为水平时接住篮球。运动员与篮球均可看成质点,篮球与地面发生作用的时间为0.02s,并认为篮球与地面接触时可看成是水平方向的匀变速运动,不计空气阻力,g取10m/s2,求甲抛球的位置与乙接球的位置之间的水平距离。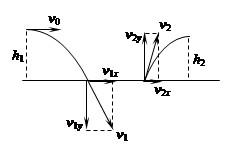
如图所示,倾角θ = 60°的粗糙平直导轨与半径为R的光滑圆环轨道相切,切点为B,轻弹簧一端固定,自由端在B点,整个轨道处在竖直平面内。现将一质量为m的小滑块(视为质点)紧靠且压缩弹簧,并从导轨上离水平地面高h = 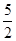 R的A处无初速下滑进入圆环轨道,恰能到达圆环最高点D,不计空气阻力。滑块与平直导轨之间的动摩擦因数μ = 0.5,重力加速度大小为g。求:
R的A处无初速下滑进入圆环轨道,恰能到达圆环最高点D,不计空气阻力。滑块与平直导轨之间的动摩擦因数μ = 0.5,重力加速度大小为g。求: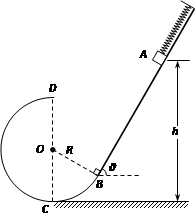
(1)滑块运动到圆环最高点D时速度υD的大小;
(2)滑块运动到圆环最低点时受到圆环轨道支持力N的大小;
(3)滑块在A处时弹簧的弹性势能Ep。
一质量m =" 500" t的机车,以恒定功率P =" 375" kW由静止出发,沿直线行驶了s = 2250m速度达到最大值υm =" 54" km/h。若机车所受阻力f恒定不变,取重力加速度g =" 10" m/s2,试求:
(1)机车受到阻力f的大小;(2)机车在这2250m内行驶所用的时间t。
某战士在倾角θ = 30°的山坡上进行投掷手榴弹训练。他从A点以某一初速度υ0沿水平方向投出手榴弹,正好落在B点,测得AB = 90m。设空气阻力不计,取重力加速度g = 10m/s2。
(1)该型号手榴弹从拉动弹弦到爆炸需要T = 5s的时间,若要求手榴弹正好在落地时爆炸,求战士从拉动弹弦到投出所用的时间△t;
(2)求手榴弹抛出的初速度υ0大小。