如图所示,一轻质弹簧两端连接着物体A和物体B,放在光滑的水平面上,水平速度为V0的子弹射中物体A并嵌在其中,已知物体B的质量为mB,物体A的质量是物体B的质量的3/4,子弹的质量是物体B的质量的1/4,求弹簧被压缩到最短时的弹性势能。
某实验小组,为了测量一个量程为0—3V的电压表的内电阻RV(约几千欧),他们采用了如下的电路完成了实验。
(1)将图2所给的实验器材按照图1所示的电路简图连接成测量电路。
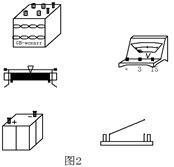
(2)测量时可以选择的实验步骤有:
A、闭合电键K;
B、将电阻箱Ro的电阻调到最大;
C、将电阻箱Ro的电阻调到零;
D、把滑动变阻器R的滑片P滑到a端;
E、把滑动变阻器R的滑片P滑到b端;
F、调节电阻箱Ro的阻值,使电压表指针指示为1.5V,记下此时电阻箱Ro的阻值;
G、调节滑动变阻器R的滑片P,使电压表的指针指示为3.0V;
H、断开电键K。
请你把必要的实验步骤选择出来,并把步骤的字母代号按照合理的操作顺序列在下面的横线上:____________________________。
(3)该实验中可供选择的实验仪器有:
A、滑动变阻器:阻值范围0~2000欧;
B、滑动变阻器:阻值范围0~20欧;
C、电阻箱:阻值范围0~9999欧;
D、电阻箱:阻值范围0~999欧;
E、电源:输出电压5V;
F、电源:输出电压2V。
本实验中,电阻箱应该选择_______,滑动变阻器应该选择______,电源应该选择______。
(4)如果在上述实验步骤F中,某一学生读出电阻箱Ro的阻值为2500欧,则实验所测电压表的内阻RV=_____________欧。该小组上述方法测出的电压表的内电阻RV与电压表的真实值相比将_________(填“相同”“偏小”或“偏大”)。
如下图有一种全自动相机的曝光时间(快门从打开到关闭的时间)是固定不变的。为了估测相机的曝光时间,有位同学提出了下述实验方案(以下忽略空气阻力):
他从坚直墙面上O点的左上方与O竖直高度相距H=5.5m处,水平弹出一个小石子落下,在小石子沿抛物线下落通过O点以后,按动快门,对小石子照相,得到如图所示的照片,由于石子的运动,它在照片上留下一条模糊的径迹AB。已知每块砖的平均长度约为24cm,平均厚度约6cm。(g取9.8m/s2)
(1)从这些信息估算该相机的曝光时间最近于()
A.0.04 s
B.0.06 s
C.0.02 s
D.0.08 s
(2)用以上信息估算出平抛的初速度m/s。
某同学做“测定电源的电动势和内阻”的实验。
(1)采用如图甲所示的实验电路进行测量,图乙给出了做实验所需要的各种仪器,请你按电路图把它们连成实验电路。
(2)这位同学测量时记录了5组数据,并将数据填入了下面表格中。请你根据这些数据在图丙中画出U—I图线。根据图线求出电池的电动势E=V,内阻r=Ω。
| 次数 |
1 |
2 |
3 |
4 |
5 |
| I/A |
0.15 |
0.25 |
0.36 |
0.45 |
0.56 |
| U/V |
1.40 |
1.35 |
1.30 |
1.25 |
1.20 |
实验室中用如图所示的电路可测量电源的电动势和内电阻实验时,先闭合开关,调节电阻箱阻值为 时,电流表的示数为
时,电流表的示数为 ;再次调节电阻箱,当阻值为
;再次调节电阻箱,当阻值为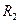 时,电流表的示数为
时,电流表的示数为 。
。
(1)若不计电流表的内阻,试利用上述物理量写出电源电动势E和内电阻r的表达式。
(2)若计电流表的内阻,从理论上分析,用上述方法测出的数据与真实值比较,电动势,内电阻(填“偏大”、“偏小”或“不变”)。
(3)实验中某同学利用测得的数据,描绘出电流的倒数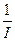 与电阻箱接入电阻R的关系图象,由图象可知该电源的电动势为V,内电阻为Ω。
与电阻箱接入电阻R的关系图象,由图象可知该电源的电动势为V,内电阻为Ω。
现有一特殊电池,它的电动势E约为9V,内阻r约为40Ω,已知该电池允许输出的最大电流为50 mA。为了测定这个电池的电动势和内阻,某同学利用如图甲所示的电路进行实验,图中电流表的内阻 已经测出,阻值为5Ω,R为电阻箱,阻值范围0~999.9Ω,
已经测出,阻值为5Ω,R为电阻箱,阻值范围0~999.9Ω, 为定值电阻,对电路起保护作用。
为定值电阻,对电路起保护作用。
(1)实验室备有的定值电阻 有以下几种规格:
有以下几种规格:
A.10Ω B.50Ω C.150Ω D.500Ω
本实验选用哪一种规格的定值电阻最好?
答:。
(2)该同学接入符合要求的 后,闭合开关S,调整电阻箱的阻值,读取电流表的示数,记录多组数据,作出了图乙所示的图线,则根据该同学作出的图线可求得该电池的电动势E=V,内阻r=Ω。
后,闭合开关S,调整电阻箱的阻值,读取电流表的示数,记录多组数据,作出了图乙所示的图线,则根据该同学作出的图线可求得该电池的电动势E=V,内阻r=Ω。