某农科院实验田里种有甲、乙两种植物,甲种植物每天施A种肥料,该种肥料的价格是3元/kg,乙种植物每天施B种肥料,该种肥料的价格是1.2元/kg.已知两种植物每天的施肥量y(kg)与时间x(天)之间都是一次函数关系.
(1)根据表中提供的信息,分别求出甲、乙两种植物每天的施肥量y(kg)与施肥时间x(天)之间的函数关系式;
(2)通过计算说明第几天使用的A种肥料与B种肥料的费用相等?
|
第1天 |
第2天 |
第3天 |
… |
||||||
| 甲种植物 |
38 |
36 |
34 |
… |
||||||
| 乙种植物 |
11 |
12 |
13 |
… |
在一个不透明的盒子中,放入2个白球和1个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出2个球,请通过列表或树状图求摸出2个球都是白球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋中,再次搅匀后从中任意摸出1个球,请通过列表或树状图求2次摸出的球都是白球的概率;
(3)现有一个可以自由转动的转盘,转盘被等分成60个相等的扇形,这些扇形除颜色外完全相同,其中40个扇形涂上白色,20个扇形涂上红色,转动转盘2次,指针2次都指向白色区域的概率为.
写出下列命题的已知、求证,并完成证明过程.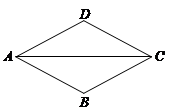
命题:如果平行四边形的一条对角线平分它的一个内角,那么这个平行四边形是菱形.
已知:如图,.
求证:.
证明:
某旅游商店有单价分别为10元、30元和50元的三种绢扇出售,该商店统计了2013年3月份这三种绢扇的销售情况,并绘制统计图如下:
请解决下列问题:
(1)计算3月份销售了多少把单价为50元的绢扇,并在图②中补全条形统计图;
(2)该商店所销售的这些绢扇的平均价格是多少呢?小亮计算这个平均价格为: (元),
(元),
你认为小亮的计算方法正确吗?如不正确,请你计算出这个平均价格.
解不等式组 ,并写出不等式组的整数解.
,并写出不等式组的整数解.