如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP=___________.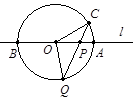
下列四个点中,有三个点在同一反比例函数 的图象上,则不在这个函数图象上的点是()
的图象上,则不在这个函数图象上的点是()
| A.(5,1) | B.(-1,5) | C.( ,3) ,3) |
D.(-3,- ) ) |
在平面直角坐标系中,已知点A(m,3)与点B(4,n)关于y轴对称,那么(m+n)2015的值为()
| A.-1 | B.1 | C.-72015 | D.72015 |
如图所示,已知点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,FG=2,则CF的长为()
A.4 B.4.5 C.5D.6
计算-(-3a2b3)4的结果是()
| A.81a8b12 | B.12a6b7 | C.-12a6b7 | D.-81a8b12 |
某市一天的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高()
| A.-10℃ | B.-6℃ | C.10℃ | D.6℃ |