某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出 100件,后来经过市场调查,发现这种商品每降低1元,其销量可增加10件。
⑴求商场经营该商品原来一天可获利润多少元?
⑵设后来该商品每件降价x元,商场一天可获利y元。
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,并通过画该函数图像的草图,观察其图象的变化趋势,结合题意写出该x取何值时,商场所获利润不少于2160元?
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为()
),则点C的坐标为()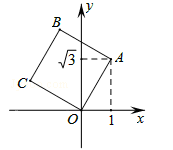
A.(﹣ ,1) ,1) |
B.(﹣1, ) ) |
C.( ,1) ,1) |
D.(﹣ ,﹣1) ,﹣1) |
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()
| A.30° | B.60° | C.90° | D.150° |
三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是()
的一个实数根,则该三角形的面积是()
| A.24 | B.24或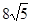 |
C.48 | D.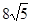 |
已知在△ABC中,AB=AC=13, BC=10,那么△ABC的内切圆的半径为()
A.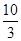 |
B. |
C.2 | D.3 |
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、 F,过点F作FG⊥FE,交直线AB于点G,若∠1=42°,则∠2的大小是()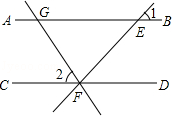
A.56° B.48° C.46° D.40°