如图所示,水平放置的轻弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长。现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为Ep= 28J。撤去推力后,P沿桌面滑到一个上表面与桌面等高且静止在光滑水平地面上的长木板Q上,已知P、Q的质量均为m=2kg,A、B间的距离L1=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求:
(1)P刚滑到Q上时的速度大小;
(2)当Q的长度为3m时,试通过计算说明P是否会滑离Q。若不会滑离,则求出P、Q的共同速度大小;若会滑离,则求出当P滑离Q时,P和Q的速度各为多大?
把一电荷量为+q、质量为m的小球放在光滑水平面上,水平面上方有一方向向东的匀强电场,用手按住小球使其静止在P点,现在突然放开手,并设法使小球突然获得一水平向西的速度v,并且在小球开始运动的同时,对小球施加一水平向北、大小为F的恒力(图中未画出),当小球向西运动到最远处的速度大小也为v,求:
(1)电场强度的大小;
(2)小球向西运动的最大距离。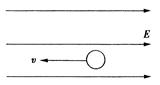
S为一离子源,它能机会均等地向MN右方空间各方向持续地大量发射相同的正离子。.离子质量为m=1×10-15kg,电量为q=2×10-8C ,速度为v0=4×105m/s。在S右侧有一半径为R=4×10-2m的圆屏,OO′是过其圆心且垂直圆面的中心轴线。(不考虑离子的重力和离子之间的碰撞效应):如果S与圆屏间有范围足够大的电场强度为E=5×106V/m的匀强电场,方向垂直屏向右.S发射的所有离子,都能打到屏上。求S与屏的最大距离。
如图所示,用一根长 为0.8m的细绳,一端拴一个质量为m的小球,另一端悬于离地面高h为2.6m处,当细绳受到3mg拉力时会被拉断,现把这小球拉到使细绳与竖直方向夹角为θ时由静止释放,若球摆到细绳竖直位置时,绳子刚好被拉断,小球平抛落到地面。求:
为0.8m的细绳,一端拴一个质量为m的小球,另一端悬于离地面高h为2.6m处,当细绳受到3mg拉力时会被拉断,现把这小球拉到使细绳与竖直方向夹角为θ时由静止释放,若球摆到细绳竖直位置时,绳子刚好被拉断,小球平抛落到地面。求:
(1)小球摆到细绳竖直位置时速度大小?
(2)夹角θ的大小;
(3)小球落地点离绳子断裂位置的水平距离s。
如图,质量m=50kg的跳水运动员从距水面高h=10m的跳台上以v0=5m/s的速度斜向上起跳,最终落入水中。若忽略运动员的身高。取g=10m/s2,求: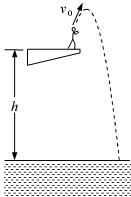
(1)运动员在跳台上时的重力势能(以水面为参考平面);
(2)运动员起跳时的动能;
(3)运动员入水时的速度大小。
北京时间2007.10.24日18:05,中国第一颗月球探测卫星“嫦娥一号”在西昌卫星发射中心由“长征三号甲”运载火箭发射升空。同学们也对月球有了更多的关注.月球绕地球运动的轨道半径r,月球绕地球的运动近似看做匀速圆周运动,试求出月球绕地球运动的周期为T。(若已知地球半径为R,地球表面的重力加速度为g)