如图所示,空间内存在水平向右的匀强电场,在虚线MN的右侧有垂直纸面向里、磁感应强度为B的水平匀强磁场,一质量为m、带电荷量为+q的小颗粒自A点由静止开始运动,刚好沿直线运动至光滑绝缘的水平面C点,与水平面碰撞后小颗粒的竖直分速度立即减为零,而水平分速度不变,小颗粒运动至D处刚好离开水平面,然后沿图示曲线DP轨迹运动,AC与水平面夹角α=37°,sin37°=0.6,cos37°=0.8,重力加速度为g,求:
(1)匀强电场的场强E;
2)AD之间的水平距离d;
(3)已知小颗粒在轨迹DP上某处达到最大速度vm,该处轨迹的曲率半径是该处距水平面高度的k倍,则该处的高度为多大?
提示:一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替。如图所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径r叫做A点的曲率半径。
如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计、质量m="2" kg的小物块,物块与小车间的动摩擦因数 ,小车足够长.求:(g取10m/s2)
,小车足够长.求:(g取10m/s2)
小物块放上时,小物块及小车的加速度各为多大?
经多长时间两者达到相同的速度?
从小物块放上小车开始,经过t=1.5s小物块通过的位移大小为多少?
北京时间2011年9月29日晚21时16分,我国在酒泉卫星发射中心载人航天发射场,用“长征二号FTl”运载火箭,将中国全新研制的首个目标飞行器“天宫一号”发射升空.如图所示,“天宫一号"首先进入近地点为A、远地点为B的椭圆轨道上,实施变轨后,又进入预定圆轨道.假设近地点A距地面高度为h,“天宫一号”在预定圆轨道上飞行n圈所甩的时间为t,地球表面的重力加速度为g,地球半径R.试求:
“天宫一号”在近地点A的加速度aA的大小;
“天宫一号”在预定圆轨道上飞行速度
 的大小.
的大小.
滑板运动已成为青少年所喜爱的一种体育运动,如图9所示,某同学正在进行滑板运动.图中AB段路面是水平的,BCD是一段半径R一20m的拱起的圆弧路面,在B点处圆滑连接,圆弧的最高点C比AB段路面高出h="1." 25m.已知人与滑板的总质量为m=60kg.该同学自A点由静止开始运动,在AB路段他单腿用力蹬地,到达B点前停止蹬地,然后冲上圆弧路段,沿圆弧到达C点,结果到达C点时恰好对地面压力为零.不计滑板与各路段之间的摩擦力及经过B点时的能量损失.求:(g取10m/s2)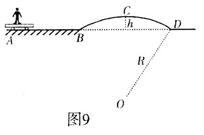
该同学到达C点时的速度.
该同学在AB段所做的功.
一个初速度是3m/s,质量是5kg的运动物体,在受到方向跟初速度方向相同、大小恒为10N的合外力作用下做匀加速运动。求:
(1)物体运动的加速度大小;
(2)运动2s末物体达到的瞬时速度大小;
(3)前2s内物体运动的位移大小。
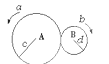
如图所示,A、B是两个靠摩擦传动且接触面没有相对滑动的靠背轮,A是主动轮,B是从动轮,它们的半径RA=2RB, a 和b两点在轮的边缘,c和d分别是A、B两轮半径的中点,下列判断正确的有
A.va =" 2" vb B.ωb = 2ωa
C.vc = va D.ac =ad