某同学准备用反证法证明如下问题:函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对于不同的x1,x2∈[0,1]都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<,那么它的假设应该是( ).
| A.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|<|x1-x2| 则|f(x1)-f(x2)|≥” |
| B.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|> |x1-x2| 则|f(x1)-f(x2)|≥” |
| C.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥” |
| D.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|>|x1-x2|时有|f(x1)-f(x2)|≥” |
.动点 到两定点
到两定点 ,
,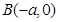 连线的斜率的乘积为
连线的斜率的乘积为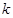 (
( ),则动点P在以下哪些曲线上()(写出所有可能的序号)
),则动点P在以下哪些曲线上()(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
| A.①⑤ | B.③④⑤ | C.①②③⑤ | D.①②③④⑤ |
若存在实数 ,使
,使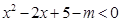 成立,则
成立,则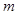 的取值范围为()
的取值范围为()
A. |
B.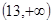  |
C.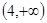 |
D.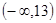 |
“ ”是“对任意的正数
”是“对任意的正数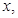 均有
均有 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
设双曲线的—个焦点为F,虚轴的—个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为 ()
A.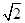 |
B.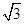 |
C.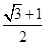 |
D. |
已知三角形ABC的面积是 ,角A,B,C成等差数列,其对应边分别是
,角A,B,C成等差数列,其对应边分别是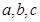 ,则
,则 的最小值是()
的最小值是()
| A.12 | B.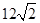 |
C. 10 | D. |