一条曲线是用以下方法画成: 是边长为1的正三角形,曲线
是边长为1的正三角形,曲线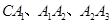 分别以
分别以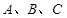 为圆心,
为圆心,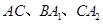 为半径画的弧,
为半径画的弧, 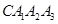 为曲线的第1圈,然后又以
为曲线的第1圈,然后又以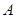 为圆心,
为圆心,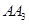 为半径画弧
为半径画弧 ,这样画到第
,这样画到第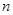 圈,则所得曲线
圈,则所得曲线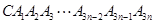 的总长度
的总长度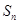 为( )
为( )
A.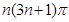 |
B.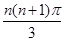 |
C.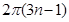 |
D.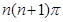 |
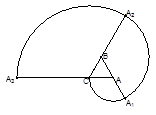
已知抛物线y2=2px(p>0)与双曲线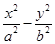 =1(a>0,b>0)有相同的焦点F,点A是两曲线的一个交点,且AF⊥x轴,则双曲线的离心率为 ( )
=1(a>0,b>0)有相同的焦点F,点A是两曲线的一个交点,且AF⊥x轴,则双曲线的离心率为 ( )
A.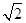 +2 +2 |
B.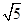 +1 +1 |
C.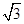 +1 +1 |
D.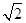 +1 +1 |
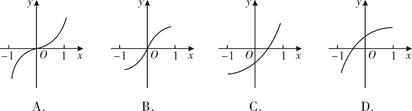
已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f ′(x)的图象如右图所示,则该函数的图象是()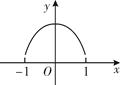
一个几何体的三视图如图所示,则该几何体的表面积是()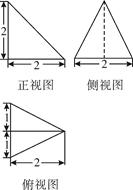
A.4+2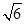 |
B.4+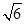 |
C.4+2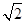 |
D.4+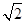 |
设函数D(x)=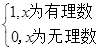 ,则下列结论错误的是()
,则下列结论错误的是()
| A.D(x)的值域为{0,1} | B.D(x)是偶函数 |
| C.D(x)不是周期函数 | D.D(x)不是单调函数 |
如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号的覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是()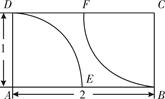
A.1- |
B.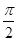 -1 -1 |
C.2-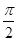 |
D. |