如图所示,固定的半圆形绝缘光滑轨道置于正交的匀强电场和匀强磁场叠加的区域中。轨道半径为R,磁感应强度为B,方向垂直于纸面向外,电场强度为E,方向水平向左。
(1)一个质量为m的小球(可视为质点)放在轨道上的C点恰好处于静止,圆弧半径OC与水平直径AD的夹角为α(sinα=0.8,cosα=0.6)。求小球所电荷量;试说明小球带何种电荷并陈述理由。
(2)如果将小球从A点由静止释放,小球在圆弧轨道上运动时,对轨道的最大压力是多少?
(3) 若将小球从A点由静止释放,小球沿圆弧轨道运动到最低点时,与另一个质量也为m且静止在O点正下方P点的不带电小球(可视为质点)发生碰撞,设碰撞过程历时可以忽略且无机械能损失也无电荷转移。两小球在运动过程中始终没有脱离圆弧轨道。求第一次碰撞后到第二次碰撞前,两小球在圆弧轨道上上升的最大高度各是多少?
质量为 =1
=1 的小物块轻轻放在水平匀速运动的传送带上的
的小物块轻轻放在水平匀速运动的传送带上的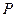 点,随传送带运动到
点,随传送带运动到 点后水平抛出,小物块恰好无碰撞的沿圆弧切线从
点后水平抛出,小物块恰好无碰撞的沿圆弧切线从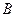 点进入竖直光滑圆孤轨道下滑。
点进入竖直光滑圆孤轨道下滑。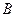 、
、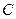 为圆弧的两端点,其连线水平,斜面与圆弧轨道在
为圆弧的两端点,其连线水平,斜面与圆弧轨道在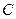 点相切连接(小物块经过
点相切连接(小物块经过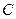 点时机械能损失不计)。已知圆弧半径
点时机械能损失不计)。已知圆弧半径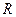 =1.0
=1.0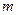 ,圆弧对应圆心角
,圆弧对应圆心角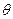 =1060,轨道最低点为
=1060,轨道最低点为 ,
, 点距水平面的高度
点距水平面的高度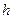 =0.8
=0.8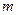 。设小物块首次经过
。设小物块首次经过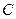 点时为零时刻,在
点时为零时刻,在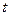 =0.8s时刻小物块经过
=0.8s时刻小物块经过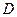 点,小物块与斜面间的滑动摩擦因数为
点,小物块与斜面间的滑动摩擦因数为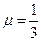 。空气阻力不计(g=10
。空气阻力不计(g=10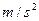 ,sin370=0.6,cos370=0.8)试求:
,sin370=0.6,cos370=0.8)试求:
(1)小物块离开 点的水平初速度%大小;
点的水平初速度%大小;
(2)小物块经过 点时对轨道的压力;.
点时对轨道的压力;.
(3)斜面上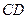 间的距离。
间的距离。
如图所示,水平放置的平行板电容器,原来两板不带电,上极板接地,它的极板长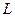 =0.1
=0.1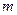 ,两板间距离
,两板间距离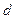 =0.4
=0.4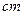 ,有一束相同微粒组成的带电粒子流以相同的初速度从两板中央平行于极板射入,由于重力作用微粒能落到下板上,已知微粒质量
,有一束相同微粒组成的带电粒子流以相同的初速度从两板中央平行于极板射入,由于重力作用微粒能落到下板上,已知微粒质量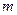 =2.0×10-6
=2.0×10-6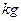 ,电量
,电量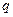 =1.0×10-8
=1.0×10-8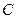 ,电容器电容
,电容器电容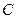 =1.0×10-6
=1.0×10-6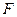 ,取g=lO
,取g=lO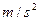 .试求:
.试求:
(1)若第一个粒子刚好落到下板中点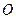 处,则带电粒子入射初速度的大小;
处,则带电粒子入射初速度的大小;
(2)两板间电场强度为多大时,带电粒子能刚好落下板右边缘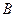 点;
点;
(3)落到下极板上带电粒子总的个数.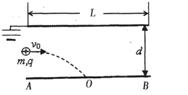
列车在机车的牵引下沿平直铁轨匀加速行驶,在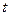 =100
=100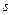 内速度由
内速度由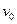 =5.0
=5.0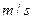 增加到
增加到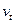 =15.O
=15.O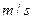 。
。
(1)求列车的加速度大小;
(2)若列车的质量是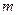 =1.0×106
=1.0×106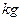 ,机车对列车的牵引力是
,机车对列车的牵引力是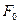 =1.5×105
=1.5×105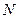 ,求列车在运动中所受的阻力大小;
,求列车在运动中所受的阻力大小;
(3)求此过程中机车牵引力做的功.
如图所示是一个设计“过山车”的试验装置的原理示意图,光滑斜面AB与竖直面内的圆形轨道在B点平滑连接,圆形轨道半径为R。一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,当它第一次经过B点进入圆形轨道时对轨道的压力为其重力的7倍,小车恰能完成圆周运动并第二次经过最低点沿水平轨道向右运动。已知重力加速度为g。
(1)求A点距水平面的高度h;
(2)假设小车在竖直圆轨道左、右半圆轨道部分克服摩擦阻力做的功相等,求小车第二次经过竖直圆轨道最低点时的速度大小。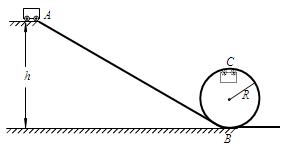
已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
(1)推导第一宇宙速度v1的表达式;
(2)若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求卫星的运行周期T。