已知数列{an}满足Sn+an=2n+1,
(1)写出a1,a2,a3,并推测an的表达式,(2)用数学归纳法证明所得的结论.
已知圆C：
内有一点P（2，2），过点P作直线
交圆C于A、B两点。
（1）当经过圆心C时，求直线的方程；
（2）当弦AB的长为
时，写出直线的方程。
已知函数
．
（1）求曲线
在点
处的切线方程；
（2）直线
为曲线的切线，且经过原点，求直线的方程及切点坐标．
已知：以点C (t, 
)(t∈R , t ≠ 0)为圆心的圆与
轴交于点O, A，与y轴交于点O, B，其中O为原点．
（1）求证：△OAB的面积为定值；
（2）设直线y = –2x+4与圆C交于点M, N，若|OM| = |ON|，求圆C的方程．
设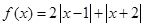
（1）求不等式
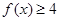的解集；
（2）若不等式
的解集是非空集合，求实数m的取值范围.
已知曲线
直线
将直线
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程；
设点P在曲线C上，求点P到直线的距离的最小值。