统计表明，某种型号的汽车在匀速行驶中每小时耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为：y=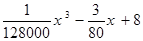
(0<x≤120).已知甲、乙两地相距100千米。
（Ⅰ）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（Ⅱ）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
（1）已知不等式ax2一bx+1≥0的解集是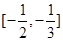
，求不等式一x2+bx+a＞0的解集；
（2）若不等式ax2+ 4x十a＞1—2x2对任意x∈R均成立，求实数a的取值范围．
己知集合A="{x" |y=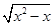
}， B={y|y=x2+x+l，x∈ R）．
（1）求A，B；（2）求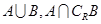
．
（本小题满分14分）
（1）已知ex≥ax +1，对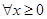
恒成立，求a的取值范围；
（2）己知
，0<x<m，求证f（x）<
．
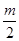（本小题满分12分）己知函数f（x）=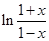 
（1）求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）求证：当x∈（0，1）时，f（x）>2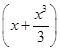
（3）设实数k使得f（x）>k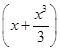对x∈（0，1）恒成立，求k的最大值．
（本小题满分12分）已知函数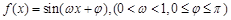
是R上的偶函数，其图象关于点M
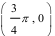对称
（1）求
的值；
（2）求
的单调递增区间；
（3）x∈
，求f（x）的最大值与最小值．