某同学准备用反证法证明如下问题:函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对于不同的x1,x2∈[0,1]都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<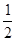 ,那么它的假设应该是( ).
,那么它的假设应该是( ).
A.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|<|x1-x2| 则|f(x1)-f(x2)|≥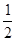 ” ” |
B.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|> |x1-x2| 则|f(x1)-f(x2)|≥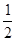 ” ” |
C.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥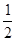 ” ” |
D.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|>|x1-x2|时有|f(x1)-f(x2)|≥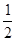 ” ” |
将函数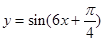 的图象上各点的横坐标伸长到原来的3倍(纵坐标不变),再向右平移
的图象上各点的横坐标伸长到原来的3倍(纵坐标不变),再向右平移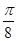 个单位,所得函数图像的一个对称中心是()
个单位,所得函数图像的一个对称中心是()
A.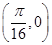 |
B.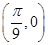 |
C.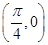 |
D.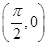 |
若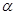 是第三象限角,且
是第三象限角,且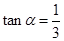 ,则
,则 ()
()
A.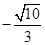 |
B.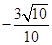 |
C.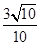 |
D.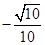 |
如下程序框图的功能是:给出以下十个数:5,9,80,43,95,73,28,17,60,36,把大于60的数找出来,则框图中的①②应分别填入的是()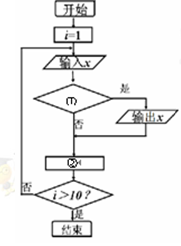
A.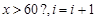 |
B.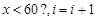 |
C.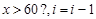 |
D.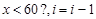 |
已知 为第三象限角,则
为第三象限角,则 所在的象限是()
所在的象限是()
| A.第一或第二象限 | B.第二或第三象限 |
| C.第一或第三象限 | D.第二或第四象限 |
下列说法中,正确的是()
| A.钝角必是第二象限角,第二象限角必是钝角 |
| B.第三象限的角必大于第二象限的角 |
C.小于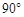 的角是锐角 的角是锐角 |
D.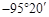 , ,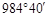 , ,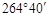 是终边相同的角 是终边相同的角 |