如图甲所示，在xoy平面内加有空间分布均匀、大小随时间周期性变化的电场和磁场，变化规律如图乙所示（规定竖直向上为电场强度的正方向，垂直纸面向里为磁感应强度的正方向）。在t=0时刻，质量m、电荷量为q的带电粒子自坐标原点O处，以v0=2m/s的速度沿x轴正向水平射出。已知电场强度E0=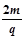
、磁感应强度B0=
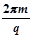，不计粒子重力。求：
（1）t=1s末粒子速度的大小和方向；
（2）1s—2s内，粒子在磁场中做圆周运动的半径和周期；
（3）画出0—4s内粒子的运动轨迹示意图（要求：体现粒子的运动特点）；
（4）（2n-1）s—2ns（n=1，2，3，，……）内粒子运动至最高点的位置坐标。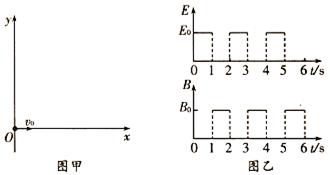
如图所示电路中，电源电动势E=10V，内阻r=1Ω，电阻R1=3Ω，R2=6Ω，R3=1Ω．求：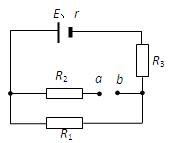
（1）在a、b间接入一只理想的电压表，它的示数为多大？
（2）在a、b间接入一只理想的电流表，它的示数为多大？
如图所示的图线，a是某电源的U—I图线，b是电阻R的图线。求：
（1）此电源的内电阻r=？
（2）若此电源和两个阻值均为R的电阻串联成闭合电路（三者均串联），则电源输出的功率P=？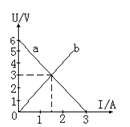
如图所示的电路中，两平行金属板A、B水平放置，两板间的距离d="40" cm．电源电动势E=24V，内电阻r=1Ω，电阻R=15Ω．闭合开关S，待电路稳定后，将一带正电的小球从B板小孔以初速度v0 = 4m/s竖直向上射入板间．若小球带电量为q =1×10-2C，质量为m=2×10-2 kg，不考虑空气阻力．那么，滑动变阻器接入电路的阻值为多大时，小球恰能到达A板？此时，电源的输出功率是多大？（取g="10" m/s2）
如图所示，直流电动机和电炉并联后接在直流电路上，电源的内阻r＝4Ω，电炉的电阻R1＝36Ω，电动机绕线的电阻R2=2Ω。当开关S断开时，电源内电路消耗的热功率P＝25W；当S闭合时，干路中的电流I=7A求：
（1）电源的电动势E．
（2）S闭合后电动机的机械功率.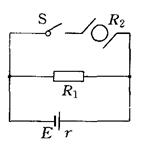
一个不带电的平行板电容器,用电压为60V的直流电源充电,充电过程中电源耗去了4.8×10-6J的能量,试求这个电容器的电容,并求在此充电过程中,从一个极板转移过程至另一个极板的电子的数目.