如图,椭圆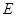 :
: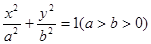 的右焦点
的右焦点 与抛物线
与抛物线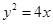 的焦点重合,过
的焦点重合,过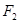 作与
作与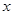 轴垂直的直线
轴垂直的直线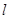 与椭圆交于S、T两点,与抛物线交于C、D两点,且
与椭圆交于S、T两点,与抛物线交于C、D两点,且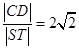 .
.
(Ⅰ)求椭圆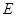 的方程;
的方程;
(Ⅱ)若过点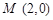 的直线与椭圆
的直线与椭圆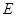 相交于两点
相交于两点 ,设
,设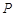 为椭圆
为椭圆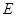 上一点,且满足
上一点,且满足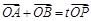 (
(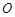 为坐标原点),当
为坐标原点),当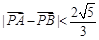 时,求实数
时,求实数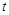 的取值范围.
的取值范围.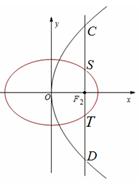
在直角坐标系 中,已知点
中,已知点 ,曲线
,曲线 的参数方程为
的参数方程为 为参数).以原点为极点,
为参数).以原点为极点, 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为
(Ⅰ)判断点 与直线
与直线 的位置关系,说明理由;
的位置关系,说明理由;
(Ⅱ)设直线 与曲线
与曲线 的两个交点为
的两个交点为 、
、 ,求
,求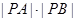 的值.
的值.
若 ,使关于
,使关于 的不等式
的不等式 在
在 上的解集不是空集,设
上的解集不是空集,设 的取值集合是
的取值集合是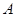 ;若不等式
;若不等式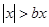
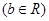 的解集为
的解集为 ,设实数
,设实数 的取值集合是
的取值集合是 ,试求当
,试求当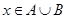 时,
时, 的值域。
的值域。
已知定直线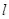 :
: ,
, ,
, 为极点,
为极点, 为
为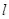 上的任意一点连接
上的任意一点连接 ,以
,以 为一边作正三角形
为一边作正三角形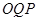 。
。 ,
, ,
, 三点按顺时针方向排列,求当点
三点按顺时针方向排列,求当点 在
在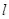 上运动时点
上运动时点 的极坐标方程,并化成直角坐标方程。
的极坐标方程,并化成直角坐标方程。
数列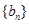 中,
中,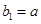 ,
, ,其中
,其中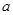 >0,对于函数
>0,对于函数 (n≥2)有
(n≥2)有 .
.
(1)求数列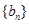 的通项公式;
的通项公式;
(2)若 ,
,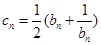 ,
, +
+ ,求证:
,求证: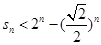
已知函数f(x)=ln(1+x)-x,g(x)=xlnx.
(1)求函数f(x)的最大值;
(2)设0<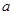 <b,证明:g(
<b,证明:g(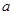 )﹢g(b)﹣
)﹢g(b)﹣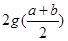 <(b﹣
<(b﹣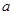 )ln2.
)ln2.