已知椭圆C: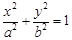 (a>0,b>0)的离心率为
(a>0,b>0)的离心率为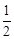 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+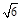 =0相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E.
=0相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:直线AE与x轴相交于定点Q;
(III)求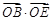 的取值范围.
的取值范围.
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.
(1)如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人,再从这8人中选3人,那么至少有一人是甲部门人选的概率是多少?
(2)若从所有甲部门人选中随机选3人,用X表示所选人员中能担任助理工作的人数,写出X的分布列,并求出X的数学期望.
已知首项都是1的两个数列{an},{bn}(bn≠0,n∈N*)满足anbn+1-an+1bn+2bn+1bn=0.
(1)令cn= ,求数列{cn}的通项公式;
,求数列{cn}的通项公式;
(2)若 ,求数列{an}的前n项和Sn.
,求数列{an}的前n项和Sn.
巳知二次函数f(x)=ax2+bx+c (a>0,b,c∈R).
(Ⅰ)已知a=2,f(2)=2,若f(x)≥2对x∈R恒成立,求f(x)的表达式;
(Ⅱ)已知方程f(x)=0的两实根 满足
满足 .设f(x)在R上的最小值为m,求证:m<x1.
.设f(x)在R上的最小值为m,求证:m<x1.
已知抛物线C:y2=2px(p>0),曲线M:x2+2x+y2=0(y>0).过点P(-3,0)与曲线M相切于点A的直线l,与抛物线C有且只有一个公共点B.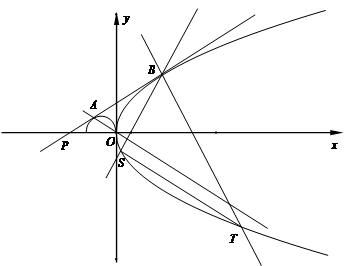
(Ⅰ)求抛物线C的方程及点A,B的坐标;
(Ⅱ)过点B作倾斜角互补的两条直线分别交抛物线C于S,T两点(不同于坐标原点),求证:直线ST∥直线AO.
设Sn为等差数列{an}的前n项和,其中a1=1,且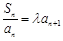 ( n∈N*).
( n∈N*).
(Ⅰ)求常数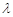 的值,并写出{an}的通项公式;
的值,并写出{an}的通项公式;
(Ⅱ)记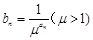 ,数列{bn}的前n项和为Tn,若对任意的n≥2,都有
,数列{bn}的前n项和为Tn,若对任意的n≥2,都有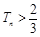 成立,求
成立,求 的取值范围.
的取值范围.