在函数概念的发展过程中,德国数学家狄利克雷(Dirichlet,1805——1859)功不可没。19世纪,狄利克雷定义了一个“奇怪的函数”: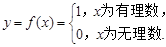 ,这个函数后来被称为狄利克雷函数。下面对此函数性质的描述中不正确的是:( )
,这个函数后来被称为狄利克雷函数。下面对此函数性质的描述中不正确的是:( )
| A.它没有单调性 | B.它是周期函数,且没有最小正周期 |
| C.它是偶函数 | D.它有函数图像 |
建立从集合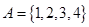 到集合
到集合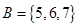 的所有函数,从中随机的抽取一个函数,其值域是B的概率为( )
的所有函数,从中随机的抽取一个函数,其值域是B的概率为( )
A.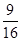 |
B.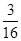 |
C.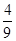 |
D. |
已知点 是圆
是圆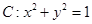 内任意一点,点
内任意一点,点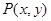 是圆上任意一点,则实数
是圆上任意一点,则实数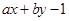 ( )
( )
| A.一定是负数 | B.一定等于0 |
| C.一定是正数 | D.可能为正数也可能为负数 |
已知函数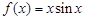 ,则
,则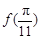 ,
, ,
,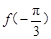 的大小关系为( )
的大小关系为( )
A.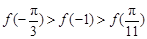 |
B. |
C.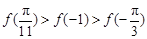 |
D. |
如图,已知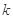 为如图所示的程序框图输出的结果,二项式
为如图所示的程序框图输出的结果,二项式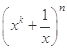 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数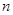 的最小值为 ()
的最小值为 ()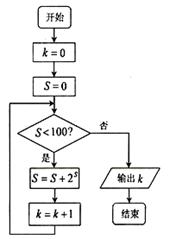
A.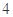 |
B.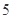 |
C.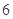 |
D.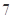 |
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②一个命题的逆命题正确,此命题的否命题不一定正确;
③线性回归方程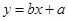 必过点
必过点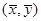 ;
;
④设随机变量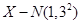 且
且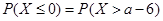 ,则实数
,则实数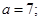
⑤ 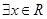 ,使得
,使得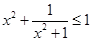 成立
成立
其中错误的个数是( )
| A.1 | B.2 | C.3 | D.4 |