某校高一年级开设研究性学习课程,(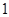 )班和(
)班和(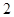 )班报名参加的人数分别是
)班报名参加的人数分别是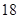 和
和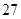 .现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从(
.现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从(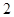 )班抽取了
)班抽取了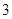 名同学.
名同学.
(Ⅰ)求研究性学习小组的人数;
(Ⅱ)规划在研究性学习的中、后期各安排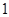 次交流活动,每次随机抽取小组中
次交流活动,每次随机抽取小组中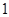 名同学发言.求
名同学发言.求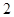 次发言的学生恰好来自不同班级的概率.
次发言的学生恰好来自不同班级的概率.
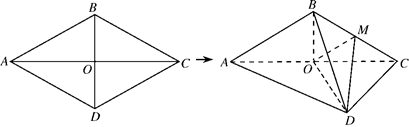
如图,菱形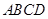 的边长为4,
的边长为4,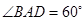 ,
,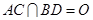 .将菱形
.将菱形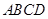 沿对角线
沿对角线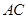 折起,得到三棱锥
折起,得到三棱锥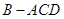 ,点
,点 是棱
是棱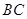 的中点,
的中点,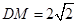 .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面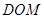
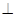 平面
平面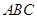 ;
;
(3)求二面角 的余弦值.
的余弦值.
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的50位顾客的相关数据,如下表所示:
一次购物量 (件) (件) |
1≤n≤3 |
4≤n≤6 |
7≤n≤9 |
10≤n≤12 |
n≥13 |
| 顾客数(人) |
 |
20 |
10 |
5 |
 |
| 结算时间(分钟/人) |
0.5 |
1 |
1.5 |
2 |
2.5 |
已知这50位顾客中一次购物量少于10件的顾客占80%.
(1)确定 与
与 的值;
的值;
(2)若将频率视为概率,求顾客一次购物的结算时间 的分布列与数学期望;
的分布列与数学期望;
(3)在(2)的条件下,若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2分钟的概率.
已知函数 ,
,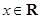 的最大值是1,最小正周期是
的最大值是1,最小正周期是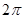 ,其图像经过点
,其图像经过点 .
.
(1)求 的解析式;
的解析式;
(2)设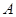 、
、 、
、 为△ABC的三个内角,且
为△ABC的三个内角,且 ,
,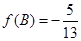 ,求
,求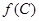 的值.
的值.
已知数列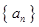 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为 ,
, 为其前n项和,且满足
为其前n项和,且满足 ,
, .数列
.数列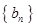 满足
满足 ,
, ,
, 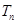 为数列
为数列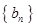 的前
的前 项和.
项和.
(1)求数列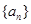 的通项公式
的通项公式 ;
;
(2)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数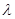 的取值范围;
的取值范围;
(3)是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有
的值;若不存在,请说明理由.
已知函数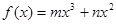 (
( ,
,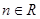 ,
,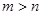 且
且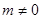 )的图象在
)的图象在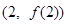 处的切线与
处的切线与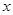 轴平行.
轴平行.
(1)确定实数 、
、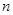 的正、负号;
的正、负号;
(2)若函数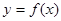 在区间
在区间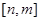 上有最大值为
上有最大值为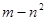 ,求
,求 的值.
的值.