如图,已知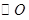 的半径是1,点C在直径AB的延长线上,
的半径是1,点C在直径AB的延长线上, 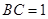 , 点P是
, 点P是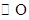 上半圆上的动点, 以
上半圆上的动点, 以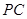 为边作等边三角形
为边作等边三角形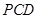 ,且点D与圆心分别在
,且点D与圆心分别在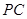 的两侧.
的两侧.
(Ⅰ) 若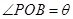 ,试将四边形
,试将四边形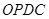 的面积
的面积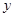 表示成
表示成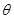 的函数;
的函数;
(Ⅱ) 求四边形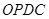 的面积的最大值.
的面积的最大值.
如图,直线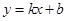 与椭圆
与椭圆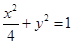 交于
交于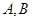 两点,记
两点,记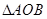 的面积为
的面积为 ,
, 是坐标原点.
是坐标原点.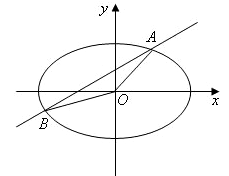
(Ⅰ)当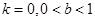 时,求
时,求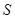 的最大值;
的最大值;
(Ⅱ)当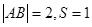 时,求直线
时,求直线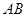 的方程.
的方程.
直线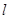 过点
过点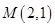 ,且与椭圆
,且与椭圆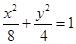 交于
交于 两点,
两点, 是坐标原点.
是坐标原点.
(Ⅰ)若点 是弦
是弦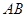 的中点,求直线
的中点,求直线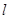 的方程;
的方程;
(Ⅱ)若直线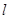 过椭圆的左焦点,求数量积
过椭圆的左焦点,求数量积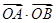 的值.
的值.
如图,已知抛物线 :
: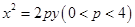 ,其上一点
,其上一点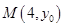 到其焦点
到其焦点 的距离为
的距离为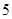 ,过焦点
,过焦点 的直线
的直线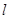 与抛物线
与抛物线 交于
交于 左、右两点.
左、右两点.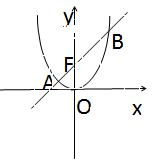
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ)若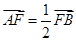 ,求直线
,求直线 的方程.
的方程.
已知圆 的半径为
的半径为 ,圆心
,圆心 在直线
在直线 上.
上.
(Ⅰ)若圆 被直线
被直线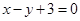 截得的弦长为
截得的弦长为 ,求圆
,求圆 的标准方程;
的标准方程;
(Ⅱ)设点 ,若圆
,若圆 上总存在两个点到点
上总存在两个点到点 的距离为
的距离为 ,求圆心
,求圆心 的横坐标
的横坐标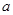 的取值范围.
的取值范围.
已知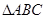 的三个顶点的坐标为
的三个顶点的坐标为 .
.
(Ⅰ)求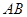 边上的高所在直线的方程;
边上的高所在直线的方程;
(Ⅱ)若直线 与
与 平行,且在
平行,且在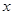 轴上的截距比在
轴上的截距比在 轴上的截距大
轴上的截距大 ,求直线
,求直线 与两条坐标轴围成的三角形的周长.
与两条坐标轴围成的三角形的周长.