设数列 的前
的前 项和为
项和为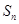 ,且对任意的
,且对任意的 ,都有
,都有 ,
, .
.
(1)求 ,
,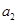 的值;
的值;
(2)求数列 的通项公式
的通项公式
已知函数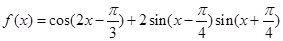 .
.
(1)求函数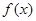 的单调递增区间;
的单调递增区间;
(2)将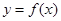 的图象向左平移
的图象向左平移 个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到
个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到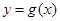 的图象;若函数
的图象;若函数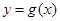 在区间
在区间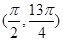 上的图象与直线
上的图象与直线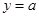 有三个交点,求实数a的取值范围.
有三个交点,求实数a的取值范围.
在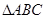 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且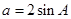 ,
,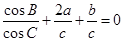 .
.
(1)求c的值;
(2)求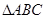 面积S的最大值.
面积S的最大值.
已知函数 ,函数
,函数
(1)当 时,求
时,求 时
时 的最大值;
的最大值;
(2)若 在
在 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)当 时,函数
时,函数 在
在 有两个不同的零点,求
有两个不同的零点,求 的取值范围.
的取值范围.
某家庭进行理财投资,根据长期收益率市场预测投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).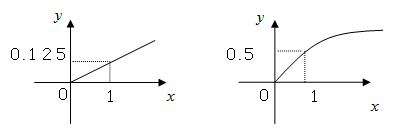
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:投资债券类产品和投资股票分别多少万元,能使投资获得最大收益,其最大收益是多少万元?
对于函数 为奇函数
为奇函数
(1)求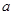 值;
值;
(2)用定义证明: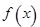 在
在 上是单调减函数;
上是单调减函数;
(3)解不等式 .
.