一小型发电机内矩形线圈在匀强磁场中以恒定的角速度ω绕垂直于磁场方向的固定轴转动,线圈匝数n=100,穿过每匝线圈的磁通量Φ随时间按正弦规律变化,如图12所示.发电机内阻 r="5.0" Ω,外电路电阻R="95" Ω,已知感应电动势的最大值Em=nωΦm,其中Φm为穿过每匝线圈的磁通量的最大值.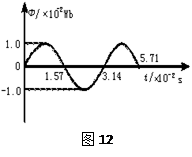
(1)最大电动势Em
(2)串联在外电路中的交流电流表(内阻不计)的读数.
如右图所示,一固定的楔形木块,其斜面的倾角为θ=30°,另一边与水平地面垂直,顶端有一个定滑轮,跨过定滑轮的细线两端分别与物块A和B连接,A的质量为4m,B的质量为m.开始时,将B按在地面上不动,然后放开手,让A沿斜面下滑而B上升,所有摩擦均忽略不计.当A沿斜面下滑距离x后,细线突然断了.求物块B上升的最大高度H.(设B不会与定滑轮相碰)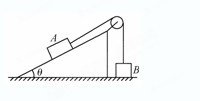
如图所示,质量M = 4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m = 1.0kg的小滑块A(可视为质点)。初始时刻,A、B分别以v0 = 2.0m/s向左、向右运动,最后A恰好没有滑离B板。已知A、B之间的动摩擦因数μ = 0.40,取g =10m/s2。求:
⑴ A、B相对运动时的加速度aA和aB的大小与方向;
⑵ A相对地面速度为零时,B相对地面运动已发生的位移x;
⑶木板B的长度l。
以速度为 =10m/s匀速行驶的汽车在第2s末关闭发动机,以后作匀减速直线运动,第3s内的平均速度是9m/s,试求:
=10m/s匀速行驶的汽车在第2s末关闭发动机,以后作匀减速直线运动,第3s内的平均速度是9m/s,试求:
⑴汽车作减速直线运动的加速度a;
⑵汽车在10s内的位移x。
如图甲所示,水平直线MN下方有竖直向上的匀强电场,场强E=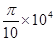 N/C。现将一重力不计、比荷
N/C。现将一重力不计、比荷 C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场。磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。
C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场。磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。
(1)求电荷进入磁场时的速度v0;
(2)求图乙中t=2×10-5s时刻电荷与P点的距离;
(3)如果在P点右方d=105 cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间(保留三位有效数字)。
如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为0.5 m,电阻忽略不计,其上端接一小灯泡,电阻为1 Ω。质量为0.2 kg的导体棒MN垂直于导轨放置,距离顶端1m,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5。在导轨间存在着垂直于导轨平面向下的匀强磁场,磁感应强度随时间变化的规律如图乙所示。先固定导体棒MN,2s后让MN由静止释放,运动一段时间后,小灯泡稳定发光。重力加速度g取10 m/s2,sin37°=0.6。求
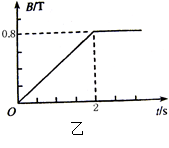
(1)1s时流过小灯泡的电流大小和方向;
(2)小灯泡稳定发光时消耗的电功率;
(3)小灯泡稳定发光时导体棒MN运动的速度。