三角形的内角平分线定理是这样叙述的：三角形一个内角的平分线分对边所成的两条线段与这个角的两边对应成比例。已知在△ABC中，∠A=60o，∠A的平分线AD交边BC于点D，设AB＝3，且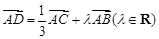
，则AD的长为（ ）
A．2 |
B． |
C．1 | D．3 |
i是虚数单位，i（1+i）等于（）
| A．1+i | B．﹣1﹣i | C．1﹣i | D．﹣1+i |
已知集合A={i，i2，i3，i4}（i为虚数单位），给出下面四个命题：
①若x∈A，y∈A，则x+y∈A；
②若x∈A，y∈A，则x﹣y∈A；
③若x∈A，y∈A，则xy∈A；
④若x∈A，y∈A，则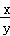
∈A．
其中正确命题的个数是（）
A.1个 B.2个 C.3个 D.4个
已知集合A={﹣1，0，1}，则（）
| A．1+i∈A | B．1+i2∈A | C．1+i3∈A | D．1+i4∈A |
i是虚数单位，复数z=i2011的虚部是（）
| A．0 | B．﹣1 | C．1 | D．﹣i |
i2011等于（）
| A．1 | B．﹣1 | C．i | D．﹣i |