已知椭圆 的中心在原点,焦点在轴 上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为 ).
(Ⅰ)求椭圆
的方程;
(Ⅱ)设点
是椭圆
的左准线与
轴的交点,过点
的直线
与椭圆
相交于
,
两点,当线段
的中点落在正方形
内(包括边界)时,求直线
的斜率的取值范围。
如图所示,D为△ABC中BC边上的一点,∠CAD=∠B,若AD=6,AB=10,BD=8,求CD的长.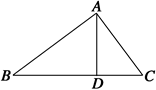
如图所示,AD、CE是△ABC中边BC、AB的高,AD和CE相交于点F.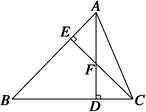
求证:AF·FD=CF·FE.
(拓展深化)如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α.且DM交AC于F,ME交BC于G,
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连接FG,如果α=45°,AB=4 ,AF=3,求FG的长.
,AF=3,求FG的长.
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.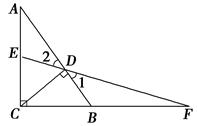
求证:FD2=FB·FC.
如图,在△ABC中,延长BC到D,使CD=BC,取AB的中点F,连接FD交AC于点E.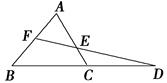
(1)求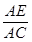 的值;
的值;
(2)若AB=a,FB=EC,求AC的长.