地球绕太阳的运动轨道可近似为圆形,若它的运行周期T的平方与其轨道半径r的立方之比为k,不计其他天体对地球的作用力,则下列关于k的说法正确的是( )
| A.k的数值只与太阳的质量有关 |
| B.k的数值只与地球的质量有关 |
| C.k的数值与地球和太阳的质量都有关 |
| D.只要知道k的数值就能求出太阳的平均密度 |
如图所示,两根长度不同的细绳,一端固定于O点,另一端各系一个相同的小球,两小球恰好在同一水平面做圆周运动,则()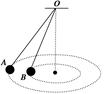
| A.它们做圆周运动的周期相等 |
| B.它们所需的向心力跟轨道半径成反比 |
| C.它们做圆周运动的线速度大小相等 |
| D.A球受绳的拉力较大 |
如图所示,两个相同的物块A、B(可视为质点),放在不光滑的水平旋转台上,A离轴距离为r,B离轴距离为2r,则圆台旋转时,下列说法正确的是()
| A.当A、B都未滑动时,A受到的静摩擦力大于B受到的静摩擦力 |
| B.当A、B都未滑动时,B受到的静摩擦力大于A受到的静摩擦力 |
| C.若圆台转速逐渐增大,则A先做离心运动 |
| D.若圆台转速逐渐增大,则B先做离心运动 |
科学家设想将来在月球上建立工作站后,可在月球上发射绕月球运行的卫星。若发射一颗月球卫星的圆轨道半径为r,运行周期为T,且已知引力常量G和月球半径R,则利用以上条件能够求出()
| A.月球上的第一宇宙速度 |
| B.月球表面的重力加速度 |
| C.卫星绕月球运行的速度 |
| D.卫星和月球的质量之比 |
在高速公路的拐弯处,通常路面都是外高内低。如图所示,在某路段汽车向左拐弯,司机左侧的路面比右侧的路面低一些。汽车的运动可看作是做半径为R的圆周运动。设内外路面高度差为h,路基的水平宽度为d,路面的宽度为L。已知重力加速度为g,要使车轮与路面之间的横向摩擦力(即垂直于前进方向)等于零,则汽车转弯时的车速应等于()

A. |
B. |
C. |
D. |
有半径为R的圆盘在水平面上绕竖直轴匀速转动,圆盘边缘上有a、b两个圆孔且在一条直线上,在圆心O点正上方高R处以一定的初速度水平抛出一小球,抛出时刻速度正好沿着Oa方向,为了让小球能准确地掉入孔中,小球的初速度和圆盘转动的角速度分别应满足(重力加速度为g)()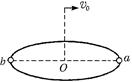
A.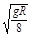 ,2kπ ,2kπ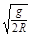 (k=1,2,3…) (k=1,2,3…) |
B.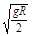 ,kπ ,kπ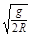 (k=1,2,3…) (k=1,2,3…) |
C.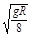 ,kπ ,kπ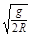 (k=1,2,3…) (k=1,2,3…) |
D.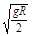 ,2kπ ,2kπ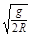 (k=1,2,3…) (k=1,2,3…) |