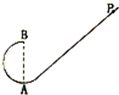
如图所示，光滑水平面上有A、B、C三个物块，其质量分别为mA=2.0kg，mB=1.0kg，mC= 1.0kg．现用一轻弹簧将A、B两物块连接，并用力缓慢压缩弹簧使A、B两物块靠近，此过程外力做108J（弹簧仍处于弹性限度内），然后同时释放A、B，弹簧开始逐渐变长，当弹簧刚好恢复原长时，C恰以4m/s的速度迎面与B发生碰撞并粘连在一起．求：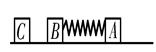
（1）弹簧刚好恢复原长时（B与C碰撞前）A和B物块速度的大小．
（2）当弹簧第二次被压缩时，弹簧具有的最大弹性势能．
做匀加速直线运动的物体途中依次经过A、B、C三点，已知AB=BC=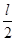
，AB段和BC段的平均速度分别为
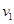=3m/s、
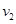=6m/s，则
（1）物体经B点时的瞬时速度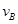
为多大？
（2）若物体运动的加速度a=2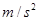
，试求AC的距离
金属硬杆轨道“ABCDEFGHIP”固定置于竖直平面内，CDE、FGH两半圆形轨道半径分别为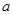
、
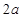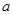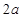，足够长的PI、AB直轨与水平均成θ=37°，一质量为m的小环套在AB杆上，环与BC、EF、HI水平直杆轨道间的动摩擦因数均为μ=0.1，其中BC=、EF=、HI=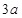
，其他轨道均光滑，轨道拐弯连接处也光滑，环通过连接处时动能损失忽略不计，现环在AB杆上从距B点
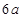处的地方无初速释放．已知sin37°=0.6，试求：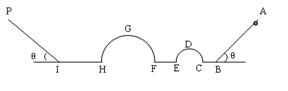
（1）从释放到第一次到达B所用的时间；
（2）第一次过小圆道轨最高点D时，环对轨道的作用力；
（3）小环经过D的次数及环最终停在什么位置？
跳伞运动员从跳伞塔上跳下，当降落伞打开后，伞和运动员所受的空气阻力大小跟下落速度的平方成正比，即Ff＝k v2，已知比例系数k ＝20N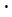
s2/m2，运动员和伞的总质量m＝72 kg．设跳伞塔足够高，且运动员跳离塔后即打开伞，取g=10m/s2．
（1）求下落速度达到v=3m/s时，跳伞运动员的加速度大小；
（2）求跳伞运动员最终下落的速度；
（3）若跳伞塔高h＝200m，跳伞运动员在着地前已经做匀速运动，求从开始跳下到即将触地的过程中，伞和运动员损失的机械能。
如图所示，一质量M为0.5kg的木块用长为L=1m的绳子悬挂着，一颗m=0.1kg的子弹以v0=20m/s的速度水平射入木块，并留在木块中。已知子弹穿入木块后子弹和木块的共同速度为v="10/3" m/s，（不计空气阻力，碰撞时间极短），试求：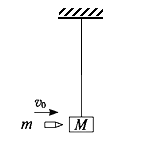
（1）在子弹射入木块过程中，系统产生的热；
（2）木块能上升的最大高度．
如图所示，在竖直平面内有一半径为R的半圆轨道与一斜面轨道平滑连接，A、B连线竖直．一质量为m的小球自P点由静止开始下滑，小球沿轨道运动到最高点B时对轨道的压力大小为mg．已知P点与轨道最高点B的高度差为2R，求小球从P点运动到B点的过程中克服摩擦力做了多少功？