一列简谐横波,如图中的实线是某时刻的波形图象,虚线是经过0.2s时的波形图象,
①若这列波向右传播,求它的最大周期?
②假定波速是35m/s,求波的传播方向?
③假定波速是35m/s,若有一质点P它的位置坐标x=0.5m,从实线对应的时刻开始计时,求经过多长时间可以到达平衡位置?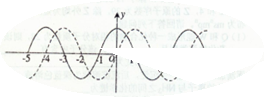
如图所示,A、B的重力分别为8牛和5牛,接触面间的动摩擦因数都是0.2,若要从B下方匀速拉出A,求所需的水平拉力F多大,系B的水平绳中的拉力多大
物体做直线运动,其位移图象如图所示,试求;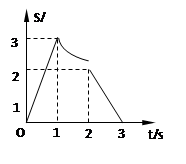
(1)5s末的瞬时速度
(2)20s内的平均速度
(3)第二个10S内的平均速度
(4)30s内的位移
空气的摩尔质量M=0.29g/mol,则空气中气体分子的平均质量为多少?成年人做一次深呼吸约吸入450cm3的空气,试估算做一次深呼吸,吸入的空气质量是多少?所吸入的气体分子数大约是多少?
铜的摩尔质量为6.4×10–2 kg/mol,密度为8.9×10 3 kg/m3,阿伏加德罗常数为6.0×1023 mol-1若每个铜原子提供一个自由电子,则铜导体中自由电子的密度为 m-3.(保留两位有效数字)
绳系着装水的水桶,在竖直平面内做圆周运动,水的质量m = 0.5kg,绳长L = 40cm,求:
(1)为使桶在最高点时水不流出,桶的最小速率?
(2)桶在最高点速率v = 3m/s时,水对桶底的压力?